Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vị trí ảnh:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{20}=\dfrac{1}{60}+\dfrac{1}{d'}\Rightarrow d'=30cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{5}{h'}=\dfrac{60}{30}\Rightarrow h'=2,5cm\)

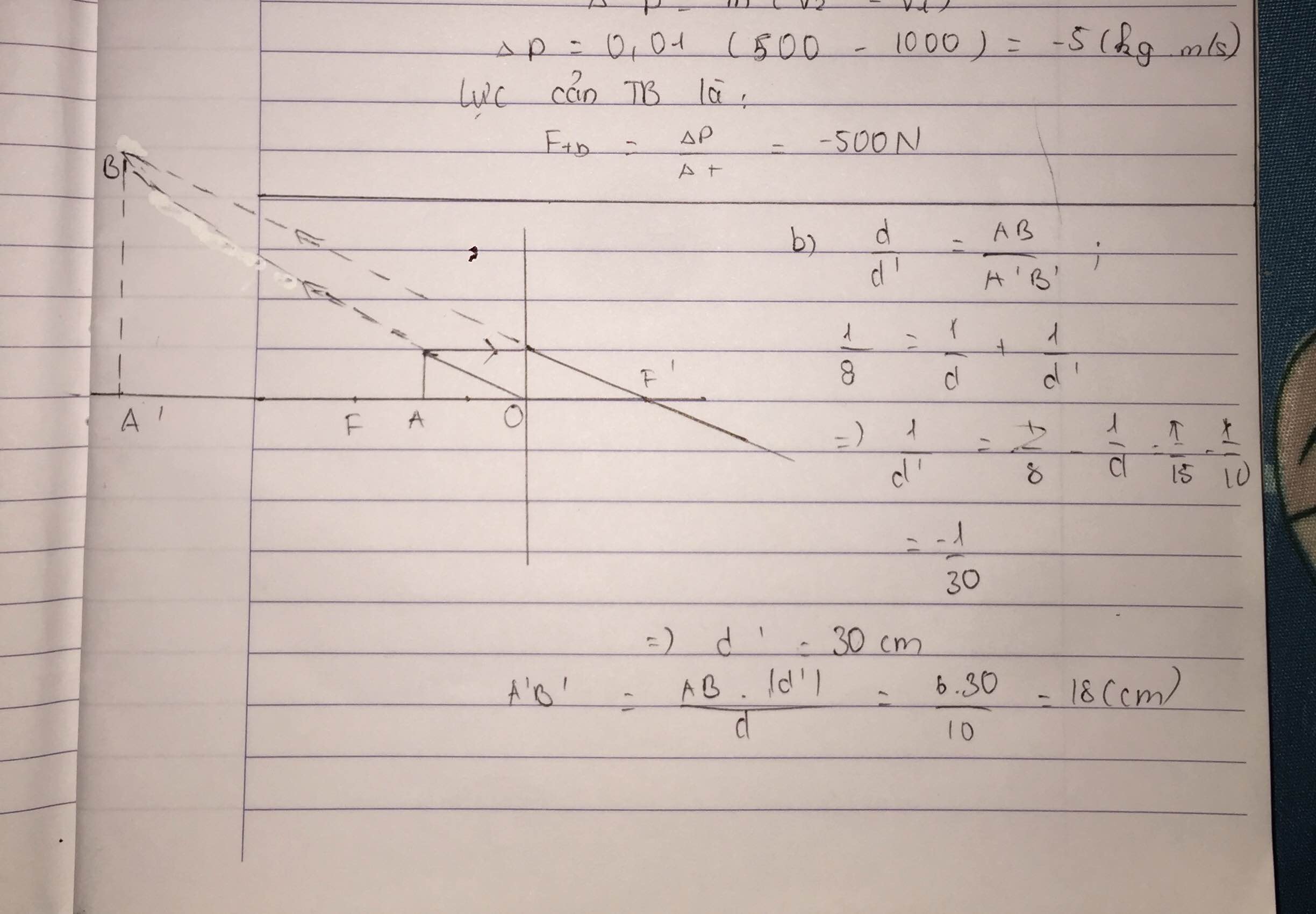
Câu 1.
Khoảng cách từ ảnh đến thấu kinh:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{d'}=\dfrac{1}{d}+\dfrac{1}{f}=\dfrac{1}{30}+\dfrac{1}{15}=\dfrac{1}{10}\)
\(\Rightarrow d'=10cm\)
Độ cao vật: \(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{h}{18}=\dfrac{30}{10}\Rightarrow h=54cm\)
Câu 2.
Bạn tự vẽ hình nha!!!
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{60}=\dfrac{1}{d'}-\dfrac{1}{40}\Rightarrow d'=24cm\)
Chiều cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{2}{h'}=\dfrac{40}{24}\Rightarrow h'=1,2cm\)

Ảnh thật, ngược chiều và lớn hơn vật.
Vị trí đặt ảnh:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{20}=\dfrac{1}{30}+\dfrac{1}{d'}\Rightarrow d'=60cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{4,5}{h'}=\dfrac{30}{60}\Rightarrow h'=9cm\)

a, vì ảnh của vật AB là ảnh ảo
mà d>f (20cm>15cm) nên Thấu kính này là thấu kính phân kì
b,c, ta có 1/f=1/d'-1/d<=>1/15=1/d'-1/20<=>d'=60/7cm
có h/h'=d/d'<=>2/h'=20.7/60=>h'=6/7cm
Vậy vị trí của ảnh cánh thấu kính 1 khoảng = d'=60/7cm
độ cao của ảnh A'B'=6/7cm
vì vật và ảnh nằm về một phía của trục chính \(\Rightarrow\) ảnh ảo
+ giả sử thấu kính được dùng là thấu kính hội tụ
vì ảnh cách vật 22,5cm \(\Rightarrow\) \(d'-d=22,5\left(cm\right)\Leftrightarrow d'=22,5+d\)
ta có \(d=\dfrac{d'f}{f+d'}\)(rút ra từ công thức \(\dfrac{1}{f}=\dfrac{1}{d}-\dfrac{1}{d'}\) với f là tiêu cự, d là khoảng cách từ vật tới thấu kính, d' là khoảng cách ảnh tới thấu kính)
\(\Leftrightarrow d=\dfrac{\left(22,5+d\right).10}{10+22,5+d}\Leftrightarrow d^2+22,5d-225=0\Leftrightarrow\left[{}\begin{matrix}d=\dfrac{15}{2}\left(tm\right)\\d=-30\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow d=30\left(cm\right)\)
độ phóng đại ảnh
\(k=\left|\dfrac{d'}{d}\right|=\dfrac{A'B'}{AB}=\dfrac{30}{\dfrac{15}{2}}=4\Rightarrow A'B'=4AB=16\left(cm\right)\)
+ giả sử thấu kính được dùng là thấu kính phân kỳ
ta có \(d-d'=22,5\Leftrightarrow d'=d-22,5\)
ta có \(d=\dfrac{d'f}{f-d'}\)(rút ra từ công thức ảnh TK phân kì \(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\))
\(\Leftrightarrow d=\dfrac{\left(d-22,5\right).10}{33,5-d}\Leftrightarrow d^2-22,5d-225\Leftrightarrow\left[{}\begin{matrix}d=30\left(tm\right)\\d=\dfrac{-15}{2}\left(loại\right)\end{matrix}\right.\Rightarrow d=30\left(cm\right)\)
\(\Rightarrow d'=\dfrac{15}{2}\left(cm\right)\)
độ phóng đại ảnh :
\(k=\left|\dfrac{d'}{d}\right|=\dfrac{A'B'}{AB}=\dfrac{\dfrac{15}{2}}{30}=\dfrac{1}{4}\Leftrightarrow A'B'=\dfrac{1}{4}AB=1\left(cm\right)\)