Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2) ta có : \(\left\{{}\begin{matrix}v_0+a\left(3-\frac{1}{2}\right)=8\\v_0+a\left(6-\frac{1}{2}\right)=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}v_0+\frac{5}{2}a=8\\v_0+\frac{11}{2}a=2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}-3a=6\\v_0+\frac{5}{2}a=8\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=-2\left(m/s^2\right)\\v_0=13m/s\end{matrix}\right.\)
=> Chọn D.
Bài1:
\(S_1=v_0.2-\frac{1}{2}.a2^2=20\)
=> \(2v_0-2a=60\)(1)
\(v^2-v_0^2=2as\Rightarrow0^2-v_0^2=2a.20\Rightarrow v_0=\sqrt{40a}\)(2)
Từ (1) và (2) => \(2.\sqrt{40a}-2a=60\)
=> \(2\left(\sqrt{40a}-a\right)=60\)
<=> \(\sqrt{40a}-a=30\)
<=> \(\sqrt{40a}=30+a\Leftrightarrow40a=a^2+60a+900\)
=> \(a^2+20a+900=0\) (pt vô nghiệm)

Bài làm:
Câu 1:
Quãng đường chiếc xe ô tô này đi được trong 2 giờ đầu là:
s1 = v1.t = 65.2 = 130 (km)
Quãng đường chiếc xe ô tô này đi được trong 2 giờ sau là:
s2 = v2.t = 45.2 = 90 (km)
⇒ Tốc độ trung bình của chiếc ô tô này trên cả quãng đường là:
vtb = \(\dfrac{s_1+s_2}{t_1+t_2}\) = \(\dfrac{130+90}{2+2}\) = 55 (km/h)
Vậy đáp án đúng là A. 55 km/h
Câu 2:
Coi bán kính của chiếc đồng hồ này dài hơn chiều dài kim giây không đáng kể và bằng 10 cm.
Chu vi của chiếc đồng hồ này là:
C = d.3,14 = r.2.3,14 = 10.2.3,14 = 62,8 (cm)
Vì đây là kim giây nên trong 1 phút hay 60 giây chiếc kim này sẽ quay hết 1 vòng, vì vậy tốc độ của kim giây trong 1 giây là:
v = \(\dfrac{s}{t}\) = \(\dfrac{62,8}{60}\) \(\approx\) 1,047 (cm/s) = 10,47.10-3 m/s
Vậy đáp án đúng là B. 10,47.10-3 m/s
Vì mình chưa học nên nhờ bạn khác giúp câu 3 nhé.
có cần lời giải không bạn ơi
Nếu không cần mình gõ đáp án trên này luôn
Nếu cần thì mình chép ra giấy cho bạn

chọn hệ trục xOy như hình vẽ ta có
các lực tác dụng lên vật là: \(\overrightarrow{Fms},\overrightarrow{F},\overrightarrow{P},\overrightarrow{N}\)
theo định luật 2 Newton ta có
\(\overrightarrow{F}+\overrightarrow{Fms}+\overrightarrow{P}+\overrightarrow{N}=\overrightarrow{a}.m\left(1\right)\)
chiếu phương trình 1 lên trục Oy ta có
-P + N=0
\(\Leftrightarrow\)P=N\(\Rightarrow\)Fms=\(\mu.N=\mu.mg\)
chiếu pt 1 lên trục Ox ta có
F-Fms=am
\(\Rightarrow\)F=am-Fms=a.m-\(\mu mg\)=1,25.10-0,3.4.10=0,5(N)
Vậy ..........
O x y P N Fms F

a)
Chọn chiều (+) hướng lên. Gốc thời gian lúc bắt đầu ném
\(y=v_0t+\frac{gt2}{2}=20t-5t^2\) (1)
\(v=v_0+gt=20-10t\) (2)
Tại điểm cao nhất v=0
Từ (2) \(\Rightarrow\) t=2(s) thay vào (1)
yM = 20(m)
b)
Khi chạm đất y=0 từ (1)\(\Rightarrow\) t=0 và t=4 (s)
Thay t = 4 (s) vào (2) \(v'=-20m\text{/}s\)
(Dấu trừ (-) vận tốc ngược với chiều dương.)

500g=0,5kg
chọn chiều dương phương thẳng đứng hướng xuống dưới
\(\overrightarrow{\Delta p}=\overrightarrow{p'}-\overrightarrow{p}\)
\(\Leftrightarrow\overrightarrow{\Delta p}=m.\overrightarrow{v_2}-m.\overrightarrow{v_1}\)
chiếu lên chiều dương
\(\Delta p=-m.sin\alpha.v_2-m.sin\alpha.v_1\)
a) với \(\alpha=30^0\)\(\Rightarrow\Delta p=\)-5kg.m/s
lực do sàn tác động lên
F=\(\dfrac{\Delta p}{\Delta t}\)=-50N
b) với \(\alpha=90^0\)\(\Rightarrow\Delta p=\)-10kgm/s
lực do sàn tác động lên
F=\(\dfrac{\Delta p}{\Delta t}\)=-100N

a, Ta có : \(T=\dfrac{1}{f}=\dfrac{1}{5}=0,2\left(s\right)\)
b, Ta có : \(C=2\pi r=0,3\pi\left(m\right)\)
\(\Rightarrow v=\dfrac{5C}{1}=\dfrac{5.0,3\pi}{1}=1,5\pi\left(m/s\right)\)
c,Ta có : \(\omega=\dfrac{2\pi}{T}=10\pi\left(rad/s\right)\)
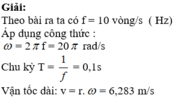

Chọn đáp án C
+ Theo bài ra ta có f = 10 vòng/s ( Hz)
+ Áp dụng công thức :
+ Chu kỳ T=1/f=0,1s
+ Vận tốc dài: v = r. ω = 6,283 m/s