Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Để xác định biên độ, tần số góc, chu kì và pha ban đầu của động, ta cần phân tích công thức của dao động và so sánh với công thức tổng quát.Công thức tổng quát của một dao động harmonic là:x = A * cos(ωt + φ)Trong đó:- x là vị trí của đối tượng tại thời điểm t.- A là biên độ của dao động.- ω là tần số góc của dao động.- t là thời gian.- φ là pha ban đầu của dao động.Trong công thức đã cho:x = -5cos(10πt + π/2)cmSo sánh với công thức tổng quát, ta có:A = -5 cm (biên độ)ω = 10π rad/s (tần số góc)φ = π/2 rad (pha ban đầu)Như vậy, biên độ của dao động là -5 cm, tần số góc là 10π rad/s, chu kì của dao động là T = 2π
2:
\(x=-3\cdot cos\left(2pi\cdot t+pi\right)\)
\(=3\cdot cos\left(pi+2pi\cdot t+pi\right)\)
\(=3\cdot cos\left(2pi\cdot t+2pi\right)\)
Biên độ là A=3
Tần số góc là 2pi
Chu kì là T=2pi/2pi=1
Pha ban đầu là 2pi
Pha của dao động tại thời điểm t=0,5 giây là;
\(2pi\cdot0.5+2pi=3pi\)
bài 1:
Biên độ góc: A = 5 cm
Tần số góc = 10 pi
Chu kì T = 2pi / tần số góc = 0,2 s
pha dao động là 10 pi x 1 - pi /2 = 19/ 2 pi
Phương trình: \(x=2cos\left(5\pi t-\dfrac{\pi}{4}\right)\)
a)Biên độ: \(A=2cm\)
Chu kì: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{5\pi}=0,4s\)
Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{0,4}=2,5Hz\)
Chiều dài quỹ đạo: \(L=2A=2\cdot2=4cm\)
b)Phương trình chất điểm:
Vận tốc: \(v=-\omega Asin\left(\omega t+\varphi\right)=-10\pi sin\left(5\pi t-\dfrac{\pi}{4}\right)\)
Gia tốc: \(a=-\omega^2Acos\left(\omega t+\varphi\right)=-500cos\left(5\pi t-\dfrac{\pi}{4}\right)\)
c)Em thay giá trị \(t=0,2s\) vào từng pt nhé.
Quỹ đạo chuyển động của con lắc thứ nhất là:
\(A_2=4\cdot A_1=4\cdot5=20\left(cm\right)\)
Phương trình dao động của con lắc thứ 2 là: \(x=20\left(cos10\pi t+\dfrac{\pi}{6}+\dfrac{\pi}{2}\right)=20\left(cos10\pi t+\dfrac{2\pi}{3}\right)\left(cm\right)\)
phương trình dao động của con lắc thứ 2:
là 20(cos10πt + \(\dfrac{2\pi}{3}\)) cm
Chu kì dao động là: \(T=\dfrac{1}{f}=\dfrac{1}{5}=0,2\left(s\right)\)
Tần số góc của dao động là: \(\omega=2\pi f=10\pi\left(rad/s\right)\)
Lúc t = 0, ta có: \(\left\{{}\begin{matrix}x=A\\v=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}cos\varphi=1\\sin\varphi=0\end{matrix}\right.\Rightarrow\varphi=0\)
Phương trình dao động là: \(x=10cos\left(10\pi t\right)cm\)
Vẽ đồ thị:
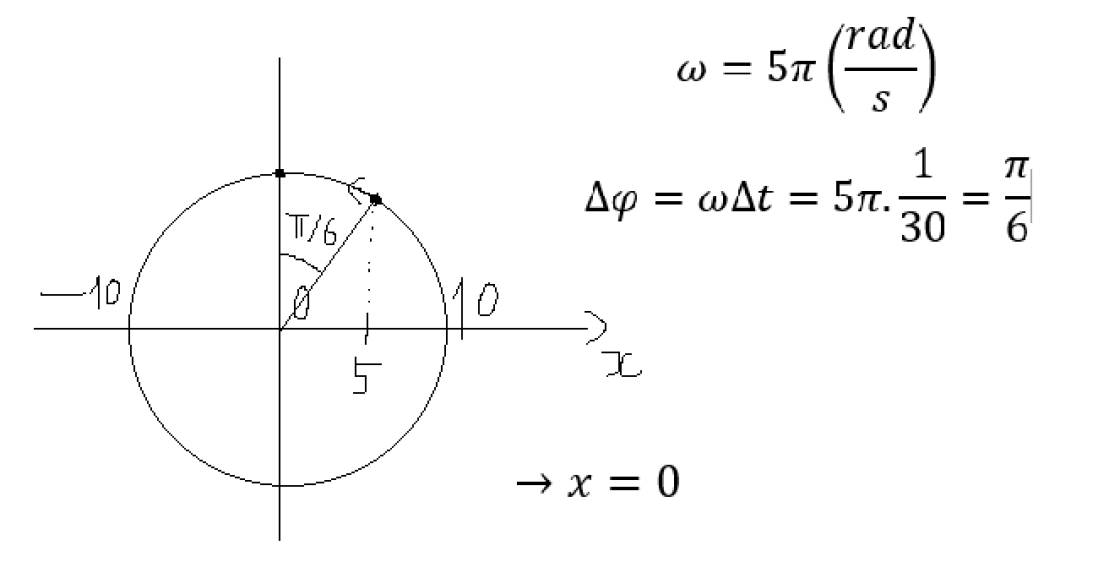
Pha dao động của phương trình là: `10 \pi t + \varphi/2`
`=>` Pha dao động tại thời điểm `1/30 s` là: `10\pi .1/30 + \varphi/2=\pi/3+ \varphi/2`.