Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Mỗi câu hỏi bạn nên hỏi 1 bài thôi để tiện trao đổi nhé.
Biểu diễn dao động bằng véc tơ quay ta có:
Để vật qua li độ 1 cm theo chiều dương thì véc tơ quay qua N.
Trong giây đầu tiên, véc tơ quay đã quay 1 góc là: \(5\pi\), ứng với 2,5 vòng quay.
Xuất phát từ M ta thấy véc tơ quay quay đc 2,5 vòng thì nó qua N 3 lần do vậy trong giây đầu tiên, vật qua li độ 1cm theo chiều dương 3 lần.
Bạn xem thêm lí thuyết phần này ở đây nhé
Phương pháp véc tơ quay và ứng dụng | Học trực tuyến
Bài 1 :
T = 2π / ω = 0.4 s
Vật thực hiện được 2 chu kì và chuyển động thêm trong 0.2 s (T/2 ) nữa
1 chu kì vật qua vị trí có li độ x=2cm theo chiều dương được "1 " lần
⇒ 2 ________________________________________... lần
phần lẻ 0.2s (T/2) , (góc quét là π ) (tức là chất điểm CĐ tròn đều đến vị trí ban đầu và góc bán kính quét thêm π (rad) nữa, vị trí lúc nầy:
x = 1 + 2cos(-π/2 + π ) = 1, (vận tốc dương) vật qua vị trí có li độ x=2cm theo chiều dương thêm 1 lần nữa
(từ VT ban đầu (vị tri +1 cm ) –> biên dương , về vị trí có ly độ x = +1 cm
do đó trong giây đầu tiên kể từ lúc t=0 vật qua vị trí có li độ x=2cm theo chiều dương được 3 lần
Chọn A
Chọn A
+ Hai dao động cùng pha
và pha φ là pha của các dao động
=> x = 15cos(πt + π/6)cm.
Ta có $x_1=x_{12}-x_2=x_{12}-(x_{23}-(x_{13}-x_1)$
$\Rightarrow$ $2x_1=x_{12}-x_{23}+x_{13}$. Bấm máy tính ta được
${x_1}={3\sqrt{6}}\cos\left({\pi t + \dfrac{\pi}{12}} \right)$
${x_3}={3\sqrt{2}}\cos\left({\pi t + \dfrac{7\pi}{12}} \right)$
Suy ra hai dao động vuông pha, như vậy khi x1 đạt giá trị cực đại thì x3 bằng 0.
cách bấm máy để ra phương trình dao động làm như thế nào vậy ạ
Chọn B
+ Áp dụng định luật bảo toàn năng lượng:
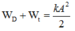
+ Động năng bằng nửa cơ năng =>
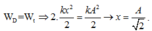
+ Trên vòng tròn lượng giác thấy cứ sau t = T/4 thì động năng lại bằng nửa cơ năng
=> T/4 = π/40 => T = π/10 (s).
+ Tại t = 0: 
=> thời điểm đầu tiên vận tốc bằng 0 là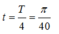 
Và cứ sau đó T/2 thì vận tốc lại bằng 0 => Tại những thời điểm vật có vận tốc bằng không là 
Đáp án B
Phương pháp: Sử dụng đường tròn lượng giác
Cách giải:
Chu kỳ dao động T = 2s
Quan sát trên hình vẽ ta thấy quãng đường vật đi được từ thời điểm t1 = 0,5s ứng với vị trí (1) đến thời điểm t2 = 1s ứng với vị trí (2) là: (5 + 5 3 ) = 13,7cm
Phương trình tổng quát: \(x = Acos(\omega t +\varphi)\)
+ Tần số góc: \(\omega = \frac{2\pi}{T}=\frac{2\pi}{2} = \pi\) (rad/s) + Biên độ: \(A=\frac{v_{max}}{\omega}=\frac{31,4}{\pi} = 10 \ (cm)\) + t = 0 \(\Rightarrow\left\{ \begin{array}{} x_0 = 5\ cm\\ v_0 <0 \end{array} \right.\) \(\Rightarrow\left\{ \begin{array}{} \cos \varphi = \frac{5}{10}=0,5\\ \sin \varphi >0 \end{array} \right. \Rightarrow \varphi = \frac{\pi}{3}\) Phương trình dao động: \(x=10\cos(\pi t + \frac{\pi}{3})\) (cm)
Chọn A
+ Quãng đường đi trong một chu kỳ là 4A => A = 10cm.
+ w = 2 π T = π ( rad / s )
+ t = 0 => x = A cos φ = 0; v = -Asin φ > 0 => φ = -π/2
Vậy: x = 10 cos ( πt - π 2 ) cm.