Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng thời gian vận tốc của vật không vượt quá \(6\pi cm/s\) là \(\frac{\Delta t}{T}=\frac{1}{3}\)
\(\Rightarrow\)Góc quét: \(\Delta\varphi=\frac{2\pi}{T}\frac{T}{3}=\frac{2\pi}{3}\left(rad\right)\)
\(\Rightarrow\) VTLG
-v
\(\Rightarrow\cos\varphi=\cos\left(90-30\right)=\frac{v}{v_{max}}=\frac{1}{2}\Rightarrow v_{max}=12\pi=\)\(\omega A\Rightarrow A=3,6cm\)

Đề bài thế này thì tổng hợp gần hết các dạng cơ bản của dao động điều hòa luôn r còn đâu :)
1/ \(v=-\omega A\sin\frac{\pi}{3}=-2\pi.5.\frac{\sqrt{3}}{2}=-5\pi\sqrt{3}\left(cm/s\right)\)
Ủa phương trình li độ x là như nào vậy? Như này ạ:\(x=5\cos\left(2\pi t-\frac{2\pi}{3}\right)?\)
2/ Câu này chả rõ ràng gì, ua li độ x=2,5 căn 3 theo chiều dương hay âm thì mới xác định được vận tốc dương hay âm chứ :(
\(A^2=x^2+\frac{v^2}{\omega^2}\Rightarrow v=\omega\sqrt{A^2-x^2}=...\left(cm/s\right)\)
3/ \(t=0\Rightarrow\left\{{}\begin{matrix}x=5\cos\frac{2\pi}{3}=-2,5\left(cm\right)\\v=-\omega A\sin\frac{2\pi}{3}< 0\end{matrix}\right.\) => Vật chuyển động theo chiều âm
Thời gian vật đi từ VTCB đến li độ \(x=-2,5\sqrt{3}\) là:
\(\Delta t_1=\frac{1}{\omega}.arc\sin\left(\frac{2,5\sqrt{3}}{5}\right)=\frac{1}{2\pi}.\frac{\pi}{3}=\frac{1}{6}\left(s\right)\)
Thời gian vật đi từ VTCB đến li độ x=-2,5 là:
\(\Delta t_2=\frac{1}{\omega}arc\sin\left(\frac{2,5}{5}\right)=\frac{1}{2\pi}.\frac{\pi}{6}=\frac{1}{12}\left(s\right)\)
\(\Rightarrow\sum t=\Delta t_1-\Delta t_2=\frac{1}{6}-\frac{1}{12}=\frac{1}{12}\left(s\right)\)
4/\(\Delta t_1=2019.T=2019.1=2019\left(s\right)\)
\(\Delta t_2=\frac{1}{\omega}.arc\cos\left(\frac{2,5}{5}\right)=\frac{1}{2\pi}.\frac{\pi}{3}=\frac{1}{6}\left(s\right)\)
\(\Delta t_3=\frac{T}{2}-\frac{1}{2\pi}arc\cos\left(\frac{2}{5}\right)=\frac{1}{2}-\frac{1}{2\pi}\frac{11}{30}\pi=\frac{19}{60}\left(s\right)\)
\(\sum t=\Delta t_1+\Delta t_2+\Delta t_3=...\)
5/ \(x=5\cos\left(2.1,125\pi-\frac{2\pi}{3}\right)\approx1,3\left(cm\right)\)
6/ \(\frac{\Delta t_2}{T}=1,25\Rightarrow\Delta t_2=T+\Delta t\Rightarrow\sum S=S_1+S_2=4A+S_2\)
\(t_1=0\Rightarrow\left\{{}\begin{matrix}x_1=-2,5\\v_1< 0\end{matrix}\right.;t_2=1,25\Rightarrow\left\{{}\begin{matrix}x_2=\frac{5\sqrt{3}}{2}\\v>0\end{matrix}\right.\)
\(\Rightarrow S_2=\frac{A}{2}+A+\frac{5\sqrt{3}}{2}=...\Rightarrow\sum S=...\)
7/ \(x=2,5\Rightarrow25=2,5^2+\frac{v^2}{4\pi^2}\Rightarrow v=2\pi\sqrt{25-2,5^2}=\pm5\pi\sqrt{3}\left(cm/s\right)\Rightarrow W_d=\frac{1}{2}mv^2=....\left(J\right)\)
8/ \(v_{tb}=\frac{S_{tb}}{t}\) Stb là uãng đường đi được trong 2,5s
Lười úa :( Tìm uãng đường đi trong 2,5s như câu 6 thui, chị tự làm nhé, có gì ko hiểu hỏi em

Chọn đáp án C.
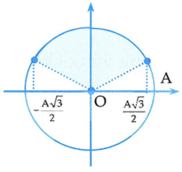
Xét vùng v 1 = π 4 v tb = π 4 . 4A T = πAω 2π = ωA 2 ⇒ x 1 = A 3 2
Vùng tốc độ ≥ v 1 khi vật chuyển động từ − x 1 đến x 1 ( hình vẽ)
⇒ Δ t = 4 T 6 = 2T 3 kết hợp với bài ta có T = 0 , 5 ( s )
Phân tích 1 6 = T 3 , quãng đuờng lớn nhất vật đi đuơc trong T/3 khi vật đi qua lân cận vị trí cân bằng
Công thức s max = 2Asin ωΔt 2 = 2Asin πΔt T = A 3 , đối chiếu với giả thiết ta có A = 2(cm)
Vận tốc cực đại của vật trong quá trình chuyển động:
v max = ωA = 2πA T = 8π(cm/s)

\(v_{max} = A\omega\)
Dựng đường tròn ứng với vận tốc
0 Aω -Aω 20π -20π φ π/3 M Q P N a b H
Cung tròn ứng với tốc độ của vật không vượt quá \(20\pi (cm/s)\) là \(\stackrel\frown{QaM} = \varphi; \stackrel\frown{NbP}= \varphi\)
=> thời gian để tốc độ (độ lớn của vận tốc) không vượt quá \(20\pi (cm/s)\) là:
\(t = \frac{2\varphi}{\omega} \)
mà giả thiết: \(t = \frac{2T}{3}s\) => \(\frac{2\varphi}{\omega} = \frac{2T}{3}\)
=> \(\varphi = \frac{2T}{3}.\frac{\omega}{2}= \frac{2\pi}{3}\) (do \(\omega = \frac{2\pi}{T}\))
=> \(\widehat{MOH} = \frac{\varphi}{2} = \frac{\pi}{3}\)
Ta có: \(\cos \widehat{MOH} =\frac{1}{2}= \frac{20\pi}{A\omega} \)
=> \(\omega = \frac{2.20\pi}{5} = 8\pi\)
=> \(T = \frac{2\pi}{\omega} =0,25s. \)
Vậy \(T= 0,25s.\)
cung tròn ko vượt quá 20pi thì là góc NOM và góc POQ chứ ??

Đáp án C.
Xét
Vùng tốc độ ≥ v 1 nằm trong - x 1 ; x 1
Phân tích 1 6 = T 3 quãng đường lớn nhất vật đi được trong T 3 khi vật đi qua lân cận vị trí cân bằng
Công thức
đối chiếu với giả thiết ta có A=2(cm)
Vận tốc cực đại của vật trong quá trình chuyển động