Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x=Acos(\(\omega t+\varphi\))
Tại thời điểm t=0, ta có:
\(\frac{A}{2}=Acos\left(\varphi\right)\) \(\Rightarrow\)\(\varphi=-\frac{\pi}{6}\)(do vật chuyển động theo chiều dương)
\(\Rightarrow\) \(x=Acos\left(\omega t-\frac{\pi}{6}\right)\)
cái này mình tưởng phải bằng: x=Acos(\(\omega t+\frac{\pi}{3}\)) chứ.

Đáp án A
Biên độ A = 8/2 = 4 cm.
Vật chuyển động nhanh dần khi vật chuyển động từ biên về cân bằng.
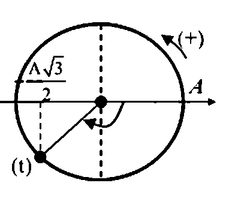
Mặt khác ta lại có khi đó vật chuyển động qua vị trí cách O 2 cm và đi theo chiều dương
→ Vật đi qua vị trí có li độ x = -4 theo chiều dương ( góc phần tư thứ 3)
Dùng đường tròn lượng giác → φ = - 2π/3 (rad).

Một vật dao động điều hòa dọc theo trục Ox. Phương trình dao động là x = 5cos(2pi*t) cm. Nếu tại một thời điểm nào đó vật đang có li độ x=3cm và đang chuyển động theo chiều dương thì sau đó 0,25s vật có li độ là:
A. -4cm
B. 4cm
C. -3cm
D.0

Đáp án A
Biên độ dao động A = MN/2 = 8 cm.
Vật chuyển động nhanh dần khi chuyển động từ biên về VTCB.
Tại t = 0 vật qua vị trí cách O 4 cm và đi nhanh dần theo chiều dương → vật có li độ x = -4 cm theo chiều dương (tức đang ở góc phần tư thứ 3).
→ Pha ban đầu của dao động là -2π/3 rad
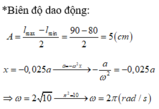
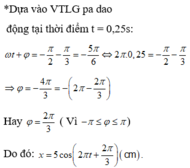

Đáp án B