Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng: \(v_{max}= \omega A \Rightarrow \omega = \frac{v_{max}}{A} = \frac{10\pi}{5} = 2\pi \ (rad/s)\)
\(\Rightarrow T = \frac{2\pi}{\omega} = 1 s\)

Giải:
\(A=\sqrt{x^2+\left(\dfrac{\upsilon}{\omega}\right)^2}=5\left(cm\right)\)
\(t=0\Rightarrow\left\{{}\begin{matrix}x=5\cos\left(\varphi\right)=0\\\upsilon=-\omega.A\sin\left(\varphi\right)< 0\end{matrix}\right.\) \(\Rightarrow\varphi=\dfrac{\pi}{2}\)
Vậy ta chọn \(C.5\cos\left(10t+\dfrac{\pi}{2}\right)cm\)
Câu 12. Một vật dao động điều hòa khi vật đi qua vị trí x = 3 cm vật đạt vận tốc 40 cm/s, biết rằng tần số góc của dao động là 10 rad/s. Viết phương trình dao động của vật? Biết gốc thời gian là lúc vật đi qua vị trí cân bằng theo chiều âm, gốc tọa độ tại vị trí cân bằng.
A. 3cos(10t + π/2) cm
B. 5cos(10t - π/2) cm
C. 5cos(10t + π/2) cm
D. 3cos(10t + π/2) cm

Combo 3 câu :)
4/ \(f=5Hz\Rightarrow\omega=10\pi\left(rad/s\right)\)
\(A^2=x^2+\frac{v^2}{\omega^2}\Leftrightarrow A=\sqrt{\left(2\sqrt{3}\right)^2+\frac{20^2\pi^2}{10^2\pi^2}}=4\left(cm\right)\)
\(2\sqrt{3}=4\cos\varphi\Rightarrow\varphi=\pm\frac{\pi}{6}\)
\(v=-20\pi< 0\Rightarrow\varphi>0\Rightarrow\varphi=\frac{\pi}{6}\)
\(\Rightarrow x=4\cos\left(10\pi t+\frac{\pi}{6}\right)\)
5/ \(A^2=\frac{a^2}{\omega^4}+\frac{v^2}{\omega^2}\Rightarrow A=\sqrt{\frac{a^2}{\omega^4}+\frac{v^2}{\omega^2}}=...\)
6/ Áp dụng công thức ở câu 5

Đáp án B
Vật đi qua vị trí có li độ là x = -2 cm và đang hướng về phía vị trí biên gần nhất nên: v = -10 cm/s
Biên độ dao động của vật: A 2 = x 2 + v 2 ω 2 = ( - 2 ) 2 + ( - 10 ) 2 5 2 ⇒ A = 2 2 cm
Tại thời điểm ban đầu:
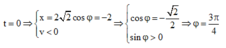
Phương trình dao động của vật là: x = 2 2 cos ( 5 t + 3 π 4 )
Chọn A