Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Fkéo = Pcos30 + Fms = mgcos30 + Fms
Fkéo = 100.10.0,5 +10 = 510N
A= F.s = 510.10 = 5100J

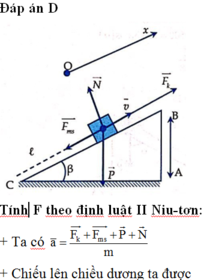
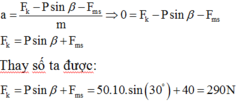
Công của lực kéo F theo phương song song với mặt phẳng nghiêng khi xe lên hết dốc là
![]()

để xe chuyển động đều (a=0)
\(\overrightarrow{F_k}+\overrightarrow{P}+\overrightarrow{N}=0\)
chiếu lên trục Ox song song với mặt phằng
Fk-sin\(\alpha\).P=0
\(\Rightarrow\)Fk=150N

TH1: Co ma sat
\(F-mg\sin30^0-\mu mg=0\Leftrightarrow F=1.10.\dfrac{1}{2}+0,1.1.10=6\left(N\right)\)
\(\Rightarrow A_F=F.s=6.0,2=1,2\left(J\right)\)
\(A_{ms}=F_{ms}.s=0,1.1.10.0,2=0,2\left(J\right)\)
\(A_P=mg\sin30^0.s=1.10.\dfrac{1}{2}.0,2=1\left(J\right)\)
TH2: Khong co ma sat
\(F=mg\sin30^0=\dfrac{10}{2}=5\left(N\right)\)
\(\Rightarrow A_F=F.s=5.0,2=1\left(J\right)=A_P\)
Các công này tính theo độ lớn, ko phải theo giá trị nên nó luôn dương

ta có : \(\overrightarrow{Fk}+\overrightarrow{Fms}+\overrightarrow{Px}+\overrightarrow{N}=0\)
chọn chiều dương theo chiều chuyển động
=> Fk - Fms - P=0
=> Fk- Fms - P.sin300 =0=> Fk= 510N=> Ak = 510.10= 5100Nm

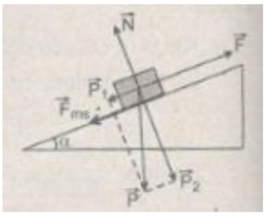
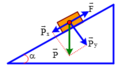
Chọn chiều chuyển động của vật m là chiều dương. Phương trình của định luật II Niu-tơn đối với vật m chuyển động trên mặt phẳng nghiêng như hình vẽ có dạng:
ma = F – P 1 - F m s
Với P 1 = mg.sin 30 ° ≈ 400 N.
F m s = μN = µmgcos 30 ° ≈ 13,8 N.
Khi vật chuyển động thẳng đều: a = 0, lực kéo có độ lớn:
F = P 1 + F m s ≈ 413,8 N
Do đó, công của lực kéo: A = Fs = 413,8.2,5 = 1034,5 J.
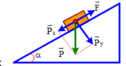
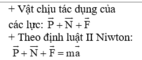

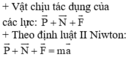
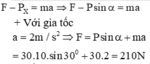
vì vật cđ đều lên dốc lên => a=0 (m/s2)
chiếu lên trục Ox: F-Fms=0 <=> F=Fms
A=F.S.cos(\(\alpha\)
=10.10.cos(30)
=\(50\sqrt{3}\) (J)