Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

giải
Công của trọng lực thực hiện từ lúc vật lên dốc đến lúc dừng lại trên dốc bằng: Ap=mgh
Với h là hiệu độ cao từ vị trí đầu đến vị trí cuối, tính theo hình ta có:

1.
theo phương pháp tổng hợp hai lực song song cùng chiều
\(F=F_1+F_2=24N\Rightarrow F_2=24-F_1=6N\) và
\(\dfrac{F_1}{F_2}=\dfrac{d_2}{d_1}\)\(\Leftrightarrow\dfrac{18}{6}=\dfrac{d_2}{30-d_2}\Rightarrow d_2=22,5cm\)
2.
. T N P -P
a)
\(sin\alpha=\dfrac{T}{P}\Rightarrow T=m.g.sin\alpha=\)24,5N
b)\(cos\alpha=\dfrac{N}{P}\Rightarrow N=\dfrac{49\sqrt{3}}{2}N\)

Đề bài không cho khối lượng nên mình cũng đang thắc mắc . Các bạn giúp mình nha.

1,
Cơ năng của vật tại vị trí thả
\(W_1=W_{đ1}+W_{t1}=mgh=0,4.10.20=80\)
thế năng ở vị trí C là
\(W_{t2}=0,4.10.15=60\)
theo định luật bảo toàn cơ năng có
\(W_{đ2}=W_{đ1}-W_{t2}=80-60=20\)

A B C D x y O N P F ms N P
vì bạn không cho hệ số ma sát trượt trên CD nên mình sẽ bỏ qua ma sát ở đoạn CD
a)theo định luật II niu tơn
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a_1}\)
chiếu lên trục xOy như hình ở GĐ1
Ox: \(sin\alpha.P-\mu.N=m.a_1\)
Oy: N=cos\(\alpha\).P
\(\Rightarrow a_1=\dfrac{sin\alpha.m.g-\mu.cos\alpha.m.g}{m}\)=\(\dfrac{24\sqrt{2}}{5}\)m/s2
vận tốc của vật khi đi hết dốc AB
v2-v02=2a1.sAB\(\Rightarrow v\approx5,21\)m/s
vận tốc của vật ở giữa dốc AB
v12-v02=2a\(\dfrac{s_{AB}}{2}\)\(\approx3,68\)m/s
b)khi xuống dốc
theo định luật II niu tơn
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a_2}\)
chiếu lên trục xOy như hình ở GĐ2
-\(\mu.m.g=m.a_2\) (N=P=m.g)
\(\Rightarrow a_2=\)-0,4m/s2
vận tốc vật khi đi đến C (\(v\approx5,21\)m/s)
v22-v2=2asBC
\(\Rightarrow\)v2\(\approx4,375\)m/s
c) theo định luật II niu tơn
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a_3}\)
chiếu lên trục xOy ở GĐ3
\(-sin\alpha.P=m.a_3\)
\(\Rightarrow a_3=\)-5m/s2
quãng đường vật đi được đến khi dừng lại (v3=0)
v32-v22=2.a3.sCD
\(\Rightarrow s_{CD}\)\(\approx1,91\)m

Fms=\(\mu\).N
N=\(P-sin\alpha.F=\)\(20-10\sqrt{2}\)N
\(\Rightarrow F_{ms}=\)\(4-2\sqrt{2}\)N
công của lực ma sát
\(A_{F_{ms}}=F_{ms}.s.cos180^0\)=\(-8+4\sqrt{2}\)J

a) theo định luật II niu tơn
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\)
chiếu lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
F.cos\(\alpha\)-\(\mu.N=0\) (1) (a=0, vật chuyển động đều)
chiếu lên trục Oy phương thẳng đứng chiều dương hướng lên trên
N=P-\(sin\alpha.F\) (2)
từ (1),(2)\(\Rightarrow F\approx103,5N\)
b) từ câu a ta có
\(F.cos\alpha-\mu.\left(P-sin\alpha.F\right)=0\)
\(\Leftrightarrow F=\dfrac{\mu.P}{cos\alpha+\mu.sin\alpha}\)
đặt \(\mu\)=\(tan\beta=\dfrac{sin\beta}{cos\beta}\) (\(0^0< \beta< 90^0\)
để F min thì MS= \(cos\alpha+\mu.sin\alpha\) max (MS: mẫu số)
\(\Leftrightarrow\)MS=\(\dfrac{cos\alpha.cos\beta+sin\beta.sin\alpha}{cos\beta}\)=\(\dfrac{cos\left(\alpha-\beta\right)}{cos\beta}\)
MS max khi \(cos\left(\alpha-\beta\right)\)=1 (vì \(cos\beta\) ở dưới mẫu min thì MS max nhưng cos\(\beta\) min ko xác định được )
\(cos\left(\alpha-\beta\right)=1\Leftrightarrow\alpha-\beta=0\)
\(\Leftrightarrow\alpha=\beta\)
\(\Rightarrow tan\alpha=tan\beta=\mu=0,2\)
\(\Rightarrow\alpha\approx11,3^0\)

Cơ năng ban đầu: \(W_1=mgh=mg.S.\sin30^0\)
Cơ năng ở chân mặt phẳng nghiêng: \(W_2=\dfrac{1}{2}mv^2\)
Bảo toàn cơ năng: \(W_1=W_2\)
\(\Rightarrow v=\sqrt{2gS.\sin 30^0}=\sqrt{2.10.10.\sin 30^0}=10(m/s)\)
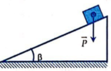

Chọn C.
Trọng lực tác dụng lên vật xác định bởi: P = mg.
Quãng đường vật di chuyển chính là chiều dài mặt phẳng nghiêng:
s = BC = 2 m
Công mà trọng lực thực hiện khi vật di chuyển hết mặt phẳng nghiêng là:
A = F.s.cosα = m.g.BC.sinβ (Vì α + β = 90o)
Thay số ta được: A = 4,9 J