Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Công của lực trác dụng lên vật chính là công cản:
\(A_{cản}=W=W_1-W_2=\dfrac{1}{2}mv^2-mgh=\dfrac{1}{2}\cdot60\cdot2^2-60\cdot10\cdot1=-480J\)

Cơ năng ban đầu: \(W_1=mgh=mg.S.\sin30^0\)
Cơ năng ở chân mặt phẳng nghiêng: \(W_2=\dfrac{1}{2}mv^2\)
Bảo toàn cơ năng: \(W_1=W_2\)
\(\Rightarrow v=\sqrt{2gS.\sin 30^0}=\sqrt{2.10.10.\sin 30^0}=10(m/s)\)

a. Ta có
sin α = 1 2 ; cos α = 3 2
Công của trọng lực
A P = P x . s = P sin α . s = m g sin α . s A P = 2.10. 1 2 .2 = 20 ( J )
Công của lực ma sát
A f m s = − f m s . s = − μ N . s = − μ . m g cos α . s A f m s = − 1 3 .2.10. 3 2 .2 = − 20 ( J )
b. Áp dụng định lý động năng
A = W d B − W d A ⇒ A P → + A f → m s = 1 2 m v B 2 − 1 2 m v A 2 ⇒ 20 − 20 = 1 2 .2 v B 2 − 1 2 .2.2 2 ⇒ v B = 2 ( m / s )
c. Áp dụng định lý động năng
A = W d C − W d B ⇒ A f → m s = 1 2 m v C 2 − 1 2 m v B 2
Công của lực ma sát
A f m s = − f m s . s = − μ N . s = − μ . m g . s / = − μ .2.10.2 = − μ 40 ( J )
Dừng lại
v C = 0 ( m / s ) ⇒ − μ 40 = 0 − 1 2 .2.2 2 ⇒ μ = 0 , 1

a)Vận tốc vật chân mặt phẳng nghiêng:
\(mgh=\dfrac{1}{2}mv^2\) (Bảo toàn cơ năng)
\(\Rightarrow v=\sqrt{2gh}=\sqrt{2\cdot10\cdot0,45}=3\)m/s
b)Độ cao vật khi \(v'=2\)m/s:
\(mgh'=\dfrac{1}{2}mv'^2\)
\(\Rightarrow h'=\dfrac{1}{2g}\cdot v'^2=\dfrac{2^2}{2\cdot10}=0,2m\)
c)Vận tốc vật khi có độ cao \(z=0,3m\):
\(mgz=\dfrac{1}{2}mv''^2\)
\(\Rightarrow v''=\sqrt{2gz}=\sqrt{2\cdot10\cdot0,3}=\sqrt{6}\)m/s

200g=0,2kg
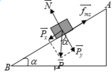
các lực tác dụng lên vật khi ở trên mặt phẳng nghiêng
\(\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)
chiếu lên trục Ox có phương song song với mặt phẳng nghiêng, chiều dương cùng chiều chuyển động
P.sin\(\alpha\)=m.a\(\Rightarrow\)a=5m/s2
vận tốc vật khi xuống tới chân dốc
v2-v02=2as\(\Rightarrow\)v=\(4\sqrt{5}\)m/s
khi xuống chân dốc trượt trên mặt phẳng ngang xuất hiện ma sát
các lực tác dụng lên vật lúc này
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a'}\)
chiếu lên trục Ox có phương nằm ngang chiều dương cùng chiều chuyển động của vật
-Fms=m.a'\(\Rightarrow-\mu.N=m.a'\) (1)
chiếu lên trục Oy có phương thẳng đứng chiều dương hướng lên trên
N=P=m.g (2)
từ (1),(2)\(\Rightarrow\)a'=-2m/s2
thời gian vật chuyển động trên mặt phẳng đến khi dừng lại là (v1=0)
t=\(\dfrac{v_1-v}{a'}\)=\(2\sqrt{5}s\)

Giải theo cách dùng định luật bảo toàn nhé.
Chọn mốc thế năng tại chân mặt phẳng nghiêng.
Độ cao của mặt phẳng nghiêng là: \(h=L\sin30^0=5m\)
Lực ma sát tác dụng lên vật: \(F_{ms}=\mu.N=\mu.mg\cos30^0=\dfrac{\sqrt 3}{2}m\)
Cơ năng khi vật ở đỉnh mặt phẳng nghiêng là: \(W_1=m.g.h=50m\)
Cơ năng khi vật ở chân mặt phẳng nghiêng: \(W_2=\dfrac{1}{2}mv^2\)
Công của ma sát là: \(A_{ms}=F_{ms}L=5\sqrt 3 m\)
Độ giảm cơ năng bằng công của lực ma sát
\(\Rightarrow W_1-W_2=A_{ms}\)
\(\Rightarrow 50m-\dfrac{1}{2}mv^2=5\sqrt 3m\)
\(\Rightarrow 50-\dfrac{1}{2}v^2=5\sqrt 3\)
Tìm tiếp để ra v nhé ![]()

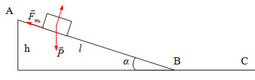
Ta có:
+ Cơ năng tại A:
\(W_A=mgh=1.9,8.1=9,8\left(J\right)\)
+ Trong khi vật chuyển động từ A đến B , tại B cơ năng chuyển hóa thành động năng tại B và công để thắng lực ma sát.
Áp dụng đl bảo toàn chuyển hóa năng lượng , ta có:
\(W_A=W_{db}-A_{Fms}\left(1\right)\)
Chọn chiều dương trùng chiều chuyển động của vật , ta có:
+ Động năng tại B : \(W_{dg}=\dfrac{1}{2}mv^2_B\)
+ Công của lực ma sát:
\(A=F_{ms}.s.cos\beta=-F_{ms}.l=-\mu P.sin\alpha.l\)
Thay vào (1) ta được:
\(W_A=W_{dB}+\left|A_{Fms}\right|\)
\(\Leftrightarrow9,8=\dfrac{1}{2}mv^2_B+\left|-\mu.P.sin\alpha.l\right|\)
\(\Leftrightarrow9,8=\dfrac{1}{2}mv^2_B\left|-\mu mg.\dfrac{h}{l}.l\right|\)
\(\Leftrightarrow9,8=\dfrac{1}{2}1.v^2_B+\left|-0,05.1.9,8.\dfrac{1}{10}.10\right|\)
\(\Rightarrow v^2_B=18,62\)
\(\Rightarrow v_B\approx4,32m/s\)
Lời giải
Chọn chiều dương là chiều chuyển động của vật, gắn hệ trục tọa độ như hình vẽ