Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x và y lần lượt là số gam đồng và kẽm có trong vật đó
(Điều kiện: x, y > 0; x < 124, y < 124 )
Vì khối lượng của vật là 124g nên ta có phương trình x + y = 124

Thể tích của x (g) đồng là 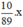 (
c
m
3
)
(
c
m
3
)
Thể tích của y (g) kẽm là 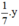 (
c
m
3
).
(
c
m
3
).
Vật có thể tích 15cm3 nên ta có phương trình: 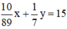
Ta có hệ phương trình:
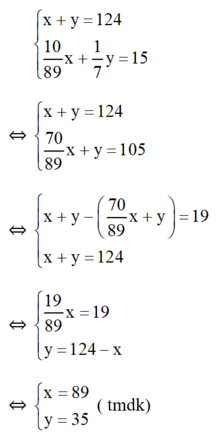
Vậy có 89 gam đồng và 35 gam kẽm.

Gọi khối lượng đồng trong hợp kim là x (0 < x < 124)
Ta có khối lượng kẽm trong hợp kim là 124 – x
Vì 89g đồng thì có thể tích là 10 c m 3 nên x (g) đồng có thể tích là 10x/89
7g kẽm thì có thể tích là 1 c m 3 nên 124 – x (g) kẽm có thể tích là (124-x)/7
Vì thể tích của hợp kim ban đầu là 15 c m 3 nên ta có phương trình:
10 x 89 + 124 - x 7 = 15 ⇔ −19x = −1691 ⇔ x = 89 (tmdk)
Vậy khối lượng đồng và kẽm trong hợp kim lần lượt là 89g và 35g
Đáp án: D

Gọi x(g) là khối lượng đồng
y (g) là khối lượng kẽm
ĐK : 0 < x,y < 124
thể tích của x(g) đồng: \(\dfrac{10}{89}\). x (\(cm^3\))
thể tích của y(g)kẽm : \(\dfrac{1}{7}.y\) (\(cm^3\))
Ta có hệ pt :
\(\left\{{}\begin{matrix}x+y=124\\\dfrac{10}{89}.x+\dfrac{1}{7}.y=15\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=124-x\\\dfrac{10}{89}.x+\dfrac{1}{7}.\left(124-x\right)=15\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=124-x\\-\dfrac{19}{623}.x=-\dfrac{19}{7}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=89\\y=124-89\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=89\\y=35\end{matrix}\right.\)
Vậy trong đó có 89 gam đồng và 35 gam kẽm

a) Với giả thiết ở đề bài, ta có thể tính được r từ đó tính được diện tích mặt cầu gần bằng \(26cm^2\)
b) Tương tự câu a, ta tính được thể tích hình nón là \(7,9cm^3\)
Gọi x và y lần lượt là số gam đồng và kẽm có trong vật đó
(Điều kiện: x, y > 0; x < 124, y < 124 )
Vì khối lượng của vật là 124g nên ta có phương trình x + y = 124
Thể tích của x (g) đồng là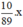 (cm3)
(cm3)
Thể tích của y (g) kẽm là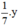 (cm3).
(cm3).
Vật có thể tích 15cm3 nên ta có phương trình: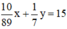
Ta có hệ phương trình:
Vậy có 89 gam đồng và 35 gam kẽm.