Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Diện tích đáy là \(12^2=144\left(cm^2\right)\)
Thể tích túi quà là: \(\dfrac{1}{3}\cdot144\cdot10=48\cdot10=480\left(cm^3\right)\)
b: Diện tích xung quanh túi quà là:
\(S_{xq}=12\cdot4\cdot12=576\left(cm^2\right)\)
Diện tích cần mua là:
\(576+12^2=720\left(cm^2\right)=0,072\left(m^2\right)\)
Số tiền cần bỏ ra là:
\(0,072\cdot200000=14400\left(đồng\right)\)

Chu vi đáy là:
8*4=32(cm)
Diện tích xung quanh là:
\(32\cdot10=320\left(cm^2\right)\)

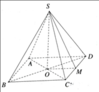
a: Gọi O là tâm của hình vuông ABCD
S.ABCD là tứ giác đều có O là tâm của đáy ABCD
=>SO là trung đoạn và SO vuông góc (ABCD)
ABCD là hình vuông
=>\(AC=BD=\sqrt{12^2+12^2}=12\sqrt{2}\left(cm\right)\)
=>\(OA=OB=OC=OD=6\sqrt{2}\left(cm\right)\)
ΔSOA vuông tại O
=>SO^2+OA^2=SA^2
=>\(SO^2=10^2-\left(6\sqrt{2}\right)^2=100-72=28\)
=>\(SO=2\sqrt{7}\left(cm\right)\)
b: \(S_{xq}=\dfrac{C_{đáy}}{2}\cdot SO\)
\(=2\sqrt{7}\cdot\left(12\cdot\dfrac{4}{2}\right)=2\sqrt{7}\cdot24=48\sqrt{7}\left(cm^2\right)\)
\(S_{tp}=48\sqrt{7}+12^2=48\sqrt{7}+144\left(cm^2\right)\)
a.
Độ dài trung đoạn của hình chóp là:
\(\sqrt{12^2-10^2}=2\sqrt{11}\left(cm\right)\)
b.
Diện tích xung quanh của hình chóp là:
\(S_{xq}=\dfrac{8.4}{2}.2\sqrt{11}.\dfrac{1}{2}=16\sqrt{11}\left(cm^2\right)\)
Diện tích toàn phần của hình chóp là:
\(S_{tp}=16\sqrt{11}+12^2=197\left(cm^2\right)\)

10: Chu vi đáy là 30*3=90(cm)
Diện tích xung quanh là \(90\cdot20=1800\left(cm^2\right)\)
=>Không có câu nào đúng
11;
\(V_{chóp}=\dfrac{1}{3}\cdot S_{đáy}\cdot h\)
=>\(\dfrac{1}{3}\cdot12\cdot S_{đáy}=100\)
=>\(S_{đáy}=25\left(cm^2\right)\)
Độ dài cạnh là \(\sqrt{25}=5\left(cm\right)\)
=>Chọn C



Để tính diện tích xung quanh của túi quà, ta sử dụng công thức:
Diện tích xung quanh = số cạnh đáy * độ dài cạnh đáy * độ dài trung đoạn
Trong trường hợp này, số cạnh đáy là 4, độ dài cạnh đáy là 12 cm, và độ dài trung đoạn là 8 cm. Thay vào công thức, ta có:
Diện tích xung quanh = 4 * 12 cm * 8 cm = 384 cm\(^2\)
Vậy diện tích xung quanh của túi quà là 384 cm\(^2\)