Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do tứ giác có hai đường chéo vuông góc tại trung điểm của mỗi đường (gt)
Suy ra tứ giác là hình thoi
Độ dài cạnh là \(52:4 = 13\) (cm)
Do hình thoi có hai đường chéo vuông góc, tạo thành 4 tam giác vuông bằng nhau.
Độ dài nửa đường chéo còn lại là: \(\sqrt {{{13}^2} - {{\left( {24:2} \right)}^2}} = \sqrt {169 - 144} = \sqrt {25} = 5\) (cm)
Độ dài đường chéo còn lại là: \(5.2 = 10\) (cm)

Ta có:
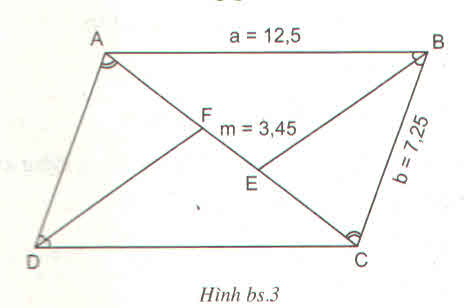
\(\widehat{ABC}=\widehat{ADC}\) và AD = BC = b = 7,25cm vì ABCD là hình bình hành.
Xét hai tam giác ADF và CBE ta có:
\(\widehat{ABC}=\widehat{ADC}\) (cmt)
AD = BC (cmt)
\(\widehat{DAF}=\widehat{BCE}\) (2 góc so le trong)
Vậy \(\Delta ADF=\Delta CBE\) (g-c-g).
=> AF = CE.
Cho AF = CE = x.
Áp dụng tính chất của đường phân giác BE trong tam giác ABC ta có:
\(\dfrac{AB}{BC}=\dfrac{AE}{CE}=\dfrac{AF+FE}{CE}\)
=> \(\dfrac{a}{b}=\dfrac{x+m}{x}=>x=\dfrac{mb}{a-b}\)= \(\dfrac{3,45.7,25}{12,5-7,25}=\dfrac{667}{140}\)
=> AC = \(2x+m=2.\dfrac{667}{140}+3,45=\dfrac{1817}{140}\approx12,98\)
Vậy AC \(\approx12,98\) cm.

a)
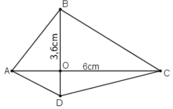
Có thể vẽ được vô số tứ giác theo yêu cầu từ đề bài. Chẳng hạn tứ giác ABCD ở hình trên.
Ta có: AC = 6cm, BD = 3,6cm và AC ⊥ BD.
Diện tích tứ giác ABCD là:
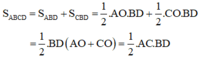
Mà AC = 6cm ; BD = 3,6 cm nên 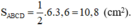
b) Hình vuông có 2 đường chéo vuông góc nên theo công thức trên, diện tích của nó là: 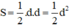

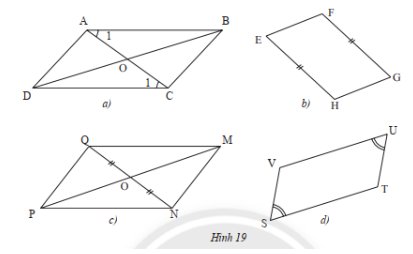
a) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
b) Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình chữ nhật.
c) Tứ giác các hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi.

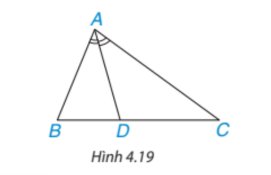
Dựa vào tính chất đường phân giác trong tam giác với tam giác ABC có AD là phân giác của góc \(\widehat{BAC}\) , ta được: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\).

Xét tam giác DBC, ta có:
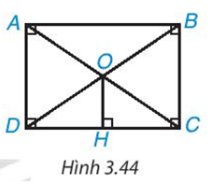
O là trung điểm cạnh BD (tính chất hình chữ nhật)
OH // BC (cùng vuông góc với CD)
⇒ OH là đường trung bình tam giác BCD.
⇒ H là trung điểm của CD (đpcm).

a: Độ dài đường chéo là \(5\sqrt{2}\left(cm\right)\)

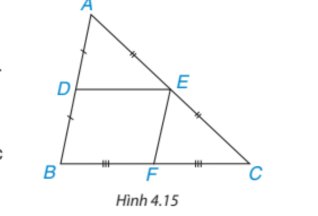
Ta có AD = BD và D ∈ AB nên D là trung điểm của AB;
AE = EC và E ∈ AC nên E là trung điểm của AC.
Xét tam giác ABC có D, E lần lượt là trung điểm của AB và AC, theo định lí Thalès đảo, ta suy ra DE // BC (đpcm).

Do tứ giác có hai đường chéo vuông góc tại trung điểm của mỗi đường (gt)
Suy ra tứ giác là hình thoi
Độ dài cạnh là \(52:4 = 13\) (cm)
Do hình thoi có hai đường chéo vuông góc, tạo thành 4 tam giác vuông bằng nhau.
Độ dài nửa đường chéo còn lại là: \(\sqrt {{{13}^2} - {{\left( {24:2} \right)}^2}} = \sqrt {169 - 144} = \sqrt {25} = 5\) (cm)
Độ dài đường chéo còn lại là: \(5.2 = 10\) (cm)