Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

n(omega)=\(C^7_{18}\)
\(n\left(\overline{A}\right)=C^7_{13}+C^7_{11}+C^7_{12}\)
=>\(P\left(A\right)=1-\dfrac{2838}{31824}=\dfrac{4831}{5304}\)

Số cách chọn 7 em bất kì trong ba khối: \(C|^7_{18}=31824\) (cách)
- Số cách chọn 7 em đi trong 1 khối:
\(C^7_7=1\) (cách)
- Số cách chọn 7 em đi trong 2 khối:
+) 7 em trong khối 12 và 11:
\(C^7_{13}-C^7_7=1715\) (cách)
+) 7 em trong khối 12 và 10:
\(C^7_{12}-C^7_7=791\) (cách)
+) 7 em trong khối 11 và 10:
\(C^7_{11}=330\) (cách)
→ Số cách chọn 7 em đi có cả ba khối:
31824 - 1 -1715 - 791 - 330 = 28987(cách)

+) Số cách chọn 3hs bất kì trong 34hs là: \(C_{34}^3\) ( cách chọn)
+) Số cách chọn 3hs nam trong 34hs là: \(C_{18}^3\) ( cách chọn)
+) Số cách chọn 3hs nữ trong 34hs là: \(C_{16}^3\) ( cách chọn)
+) Số cách chọn 3hs gồm cả nam và nữ trong 34hs là: \(C_{34}^3 - C_{18}^3 - C_{16}^3 = 4608\) ( cách chọn)

a) Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:
900.5 + 8x = 4 500 + 8x (nghìn đồng).
Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:
1 500.2 + 10y = 3 000 + 10y (nghìn đồng).
Tổng số tiền ông An phải trả cho việc thuê xe trong một tuần là:
4 500 + 8x + 3 000 + 10y = 7 500 + 8x + 10y (nghìn đồng).
Để tổng số tiền ông An phải trả không quá 14 triệu đồng thì
7 500 + 8x + 10y ≤ 14 000
⇔ 8x + 10y ≤ 6 500.
⇔ 4x + 5y ≤ 3 250.
Vậy bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng là 4x + 5y ≤ 3 250.
b)
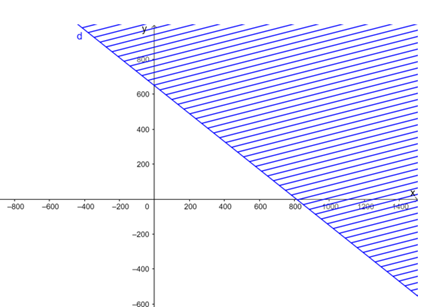
Vẽ đường thẳng d: 4x + 5y = 3 250 trên mặt phẳng tọa độ.
Lấy gốc tọa độ O(0; 0) và tính 4.0 + 5.0 = 0 < 3 250.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d không chứa gốc tọa độ và cả đường thẳng d (miền không bị gạch kể cả biên)
Tham khảo:
a)
Ta có 14 triệu = 14 000 (nghìn đồng)
Phí cố định là: 900.5 + 1500.2 = 7500 (nghìn đồng)
Phí tính theo quãng đường là:
x km trong các ngày từ thứ Hai đến thứ Sáu là 8x (nghìn đồng)
y km trong 2 cuối tuần là 10y (nghìn đồng)
Tổng số tiền ông An phải trả là 8x+10y +7500 (nghìn đồng)
Vì số tiền không quá 14 triệu đồng nên ta có :
\(\begin{array}{l}8x + 10y +7500 \le 14000\\ \Leftrightarrow 4x + 5y \le 3250\end{array}\)
Vậy bất phương trình cần tìm là \(4x + 5y \le 3250\)
b)
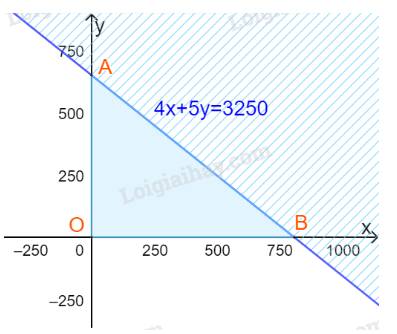
Bước 1: Vẽ đường thẳng \(4x + 5y = 3250\)(nét liền)
Bước 2: Thay tọa độ điểm O(0;0) vào biểu thức 4x+5y ta được:
4.0+5.0=0<3250
=> Điểm O thuộc miền nghiệm
=> Miền nghiệm là nửa mặt phẳng bờ là đường thẳng \(4x + 5y = 3250\) và chứa gốc tọa độ và (x;y) nằm trong miền tam giác OAB kể cả đoạn AB.

Tham khảo:
Gọi X là tập hợp các học sinh của lớp 10C.
A là tập hợp các học sinh tham gia cuộc thi vẽ đồ họa trên máy tính,
B là tập hợp các học sinh tham gia cuộc thi tin học văn phòng cấp trường.
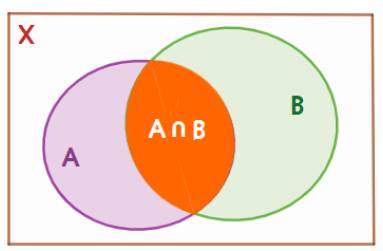
Theo biểu đồ Ven ta có: \(n(A) = 18,\;n(B) = 24,\;n(X) = 45.\)
\(n(A \cup B)\) là số học sinh tham gia ít nhất một trong hai cuộc thi, bằng: 45 -9 = 36 (học sinh)
Mà \(n(A \cup B) = n(A) + n(B) - n(A \cap B)\) (do các học sinh tham gia cả 2 cuộc thi được tính hai lần)
Suy ra số học sinh tham gia cả 2 cuộc thi là: \(n(A \cap B) = 18 + 24 - 36 = 6\)
Vậy có 6 học sinh của lớp 10C tham gia đồng thời hai cuộc thi.

gọi x à quãng đường ô tô đi được
x-50 là quãng đường xe máy đi được
Theo đề bài ta có:
30%x=45%(x-50)
<=>30%x-45%x=-22,5
<=>-0,15x=-22,5
<=> x =155 (km)
Vậy quãng đường ô tô đi được là 150 km
quãng đường xe máy đi đupợc là 150-50=100(km)

Số học sinh tham gia các câu lạc bộ khác chiếm số phần trăm là :
100% - 96,875% = 3,125%
Số học sinh tham gia câu lạc bộ khác của trường Tiểu học Thành công là :
775 : 96,875 x 3,125 = 25 học sinh
Đáp số : 25 học sinh
1. Coi số tổng số h/s là 100%
Số h/s ytung bình chiếm số phần trăm là: 100%-(35%+60%)=5%
Trường đó có số h/s trung bình là: 640:100x5=32(học sinh)
2. Diện tích mảnh đất đó là: 20x15=300(m2)
Diện tích phần đất xây nhà là: 300:100x32,5=97,5(m2)
Diện tích phần đất làm đường đi là: 300:100x22,5=67,5(m2)
Diện tích phần đất xây nhà và làm đường đi là: 97,5+67,5=165(m2)
3. Cửa hàng có số gạo là: 600x100:31,25=1920(kg)
4. Số học sinh tham gia clb tiếng anh là: 775:96,875x100=800(học sinh)
Số học sinh tham gia clb khác là: 800-775=25(học sinh)
VÌ BÀI DÀI NÊN TUI KO ĐÁP SỐ, PHẦN TUI GẠCH CHÂN LÀ ĐÁP SỐ NHA!
CHÚC BẠN HỌC TỐT NHA!
Mỗi ô tô chở được:
120 : 3 = 40 (học sinh)
Số ô tô để chở học sinh đợ thứ hai là:
160 : 40 = 4 (ô tô)
Đáp số: 4 ô tô.
1 xe ô tô chở được số học sinh là :
120 : 3 = 40 ﴾ học sinh ﴿
Trong đợt hai , muốn chở 160 học sinh cần :
160 : 40 = 4 ﴾ xe ô tô ﴿
Đáp số : 4 ô tô