Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Thể tích không khí trong chiếc lều là: \(\frac{1}{3}{.3^2}.2,8 = 8,4\) (\({m^3}\))
b) Độ dài trung đoạn của hình chóp là: \(\sqrt {2,{8^2} + 1,{5^2}} \approx 3,18\)
Diện tích vải lều là: \(\frac{{4.3}}{2}.3,18= 19,08\) (\(c{m^2}\))

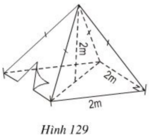
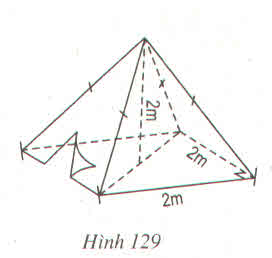
a) Lều là hình chóp đều có đáy là hình vuông cạnh bằng 2m, chiều cao bằng 2m.
Thể tích không khí trong lều bằng thể tích lều và bằng:
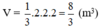
b) Số vải bạt cần thiết đề dựng lều chính là diện tích xung quanh của lều.
Dựng trung đoạn SH.
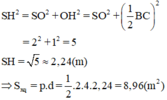

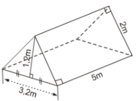
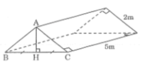
a) Lều là lăng trụ đứng tam giác.
Diện tích đáy (tam giác):
S=12.3,2.1,2=1,92(m2)S=12.3,2.1,2=1,92(m2)
Thể tích khoảng không bên trong lều là:
V = Sh = 1,92. 5 = 9,6 (m3)
b) Số vải bạt cần có để dựng lều chính là diện tích toàn phần của lăng trụ trừ đi diện tích mặt bên có kích thước là 5m và 3,2m.
Diện tích xung quanh lăng trụ là:
Sxq = 2ph = (2 + 2+ 3,2) .5 = 36 (m2)
Diện tích toàn phần:
Stp = Sxq + 2Sđ = 36 + 2.1,92 = 39,84 (m2)
Diện tích mặt bên kích thước 5m và 3,2m là:
S = 5.3,2 = 16 (m2)
Vậy số vải bạt cần có để dựng lều là:
39,84 – 16 = 23,84 (m2)
Chú ý:Có thể tính bằng cách khác là tổng diện tích hai mặt bên và hai đáy.

Diện tích vải lều cần phủ kín các mặt bên:
S = 4 . 3 . 3,2 : 2 = 19,2 (m²)

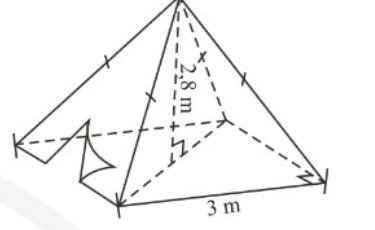
Thể tích cần tính bằng thể tích của hình chóp có chiều cao 2cm
Đáy là hình vuông cạnh dài 2m. Diện tích đáy Sđ = 22 = 4(m2)
Thể tích hình chóp : V = 1313.S.h = 1313.4.2 = 8383
b) Số vải bạt cần tính chính là diện tích của bốn mặt (hay là diện tích xung quanh) mỗi mặt là một tam giác cân.
Để tính diện tích xung quanh ta cần phải tính được trung đoạn tức là đường cao SH của mỗi mặt
SH2 = SO2 + OH2 = SO2+ (BC2)2(BC2)2 = 22 + 12 = 5
SH = √5 ≈ 2,24m
Nên Sxq = p.d = 1212 2.4.2.24 = 8,96 (m2)
Thể tích cần tính bằng thể tích của hình chóp có chiều cao 2cm
Đáy là hình vuông cạnh dài 2m. Diện tích đáy Sđ = 22 = 4(m2)
Thể tích hình chóp : \(V=\dfrac{1}{3}.S.h=\dfrac{1}{3}.4.2=\dfrac{8}{3}\)

b) Số vải bạt cần tính chính là diện tích của bốn mặt (hay là diện tích xung quanh) mỗi mặt là một tam giác cân.
Để tính diện tích xung quanh ta cần phải tính được trung đoạn tức là đường cao SH của mỗi mặt
\(SH^2=SO^2+OH^2=SO^2+\left(\dfrac{BC}{2}\right)^2=2^2+1^2=5\)
\(SH=\sqrt{5}\approx2,24m\)
Nên Sxq = p.d = \(\dfrac{1}{2}\) 2.4.2.24 = 8,96 (m2)

Số vải cần để làm lều là hai mặt bên và hai đầu hồi (hai đáy của lăng trụ đứng)
Diện tích hai mặt bên là : (2.5).2=20 ( m 2 )
Diện tích vải cần dùng là:20+2.2=24 ( m 2 )

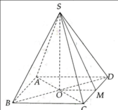
Trại có dạng hình chóp tứ giác đều S.ABCD (như hình vẽ)
a) Độ dài cạnh của trại là: CD = 3(m). Gọi O là tâm của đáy và M là trung điểm của cạnh đáy CD.
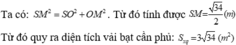
b) Thể tích của trại là:




\(a,\)
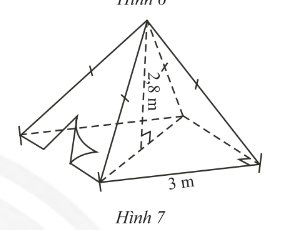
Lều có dạng hình chóp tứ giác đều có chiều cao SA
\(\rightarrow\) Đỉnh hình chóp là S, A là tâm của đáy (đáy là hình vuông)
Gọi đáy là hình vuông MNPQ
\(\rightarrow A\) là giao điểm của MP, NQ
Bán kính đường tròn ngoại tiếp đáy là 6cm
\(\rightarrow AM=AN=AP=AQ=6cm\)
\(\rightarrow MP=NQ=2.6=12cm\)
\(S_{MNPQ}=\dfrac{1}{2}.MP.NQ=\dfrac{1}{2}.12.12=72cm^2\)
Vậy thể tích không khí trong lều là:
\(V=\dfrac{1}{3}.S_{MNPQ}.SA=\dfrac{1}{3}.72.9=216cm^3\)
\(b,\)
Kẻ trung đoạn SH của mặt bên SPN \(\rightarrow\) H là trung điểm PN
\(\Delta ANP\) vuông ở A \(\rightarrow NP^2=AN^2+AP^2\rightarrow NP^2=6^2+6^2\rightarrow NP=6\sqrt{2}cm\)
Ta có: AH là đường trung tuyến \(\rightarrow AH=\dfrac{1}{2}.NP=\dfrac{1}{2}.6\sqrt{2}=3\sqrt{2}cm\)
\(\Delta SAH\) vuông ở A \(\rightarrow SH^2=AH^2+SA^2\rightarrow SH^2=\left(3\sqrt{2}\right)^2+9^2\rightarrow SH=3\sqrt{11}cm\)
\(P_{MNPQ}=C_{MNPQ}=4.NP=4.6\sqrt{2}=24\sqrt{2}cm\)
Vậy số vải bạt cần dùng để dựng chiếc trại đó là:
\(S_{xq}=\dfrac{1}{2}.C_{MNPQ}.SH=\dfrac{1}{2}.24\sqrt{2}.3\sqrt{11}=36\sqrt{22}cm^2\)