Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Việc chọn một quả dưa hấu hoặc một quả thanh long được thực hiện qua 2 phương án
Phương án 1: Chọn một quả dưa hấu, có 6 cách thực hiện
Phương án 2: Chọn một quả thanh long, có 15 cách thực hiện
Áp dụng quy tắc cộng, số cách chọn một quả dưa hấu hoặc một quả thanh long là
\(6 + 15 = 21\) (cách chọn)
b) Việc chọn một quả dưa hấu và một quả thanh long được thực hiện qua 2 công đoạn:
Công đoạn 1: Chọn một quả dưa hấu, có 6 cách thực hiện
Công đoạn 2: Chọn một quả thanh long, có 15 cách thực hiện
Áp dụng quy tắc nhân, số cách chọn một quả thanh long và một quả dưa hấu là
\(6.15 = 90\) (cách chọn)

Tổng số khả năng có thể xảy ra của phép thử là \(n\left( \Omega \right) = C_{13}^2.13\)
a) Biến cố “Ba quả bóng lấy ra cùng màu” xảy ra khi hai lần đều lấy ra bóng có cùng màu xanh, đỏ hoặc vàng. Số kết quả thuận lợi cho biến cố là \(C_5^2.5 + C_6^2.6 + C_2^2.2 = 142\)
Vậy xác suất của biến cố “Ba quả bóng lấy ra cùng màu” là \(P = \frac{{142}}{{13C_{13}^2}} = \frac{{71}}{{507}}\)
b) Số kết quả thuận lợi cho biến cố “Bóng lấy ra lần 2 là bóng xanh” là \(C_{13}^2.5\)
Vậy xác suất của biến cố “Bóng lấy ra lần 2 là bóng xanh” là \(P = \frac{{5C_{13}^2}}{{13C_{13}^2}} = \frac{5}{{13}}\)
c) Biến cố “Ba bóng lấy ra có ba màu khác nhau” xảy ra khi hai quả bóng lấy ra lần đầu là 2 màu khác nhau và quả bóng lấy lần 2 có màu còn lại. Số kết quả thuận lợi cho biến cố này là \(5.6.2.3 = 180\)
Vậy xác suất của biến cố “Ba bóng lấy ra có ba màu khác nhau” là \(P = \frac{{180}}{{13C_{13}^2}} = \frac{{30}}{{169}}\)
Cái này nhân 3 TH thui
VD (xanh+đỏ; vàng) ; (xanh+vàng; đỏ); (đỏ+vàng;xanh) nên x3 chứ không phải nhân 3! á em (câu c)

Ta thấy hai biến cố :”Hai quả bóng lây ra cùng màu” và “Hai quả bóng lấy ra khác màu” là hai biến cố đối
Suy ra xác suất của biến cố “Hai quả bóng lây ra cùng màu” là \(1 - 0,6 = 0,4\)

Gọi x và y lần lượt là giá tiền mỗi quả quýt và mỗi quả cam. (x > 0; y > 0)
Vân mua 10 quả quýt, 7 quả cam hết 17800 đồng nên ta có:
10x + 7y = 17800
Lan mua 12 quả quýt, 6 quả cam hết 18000 đồng nên ta có:
12x + 6y = 18000
Từ đó ta có hệ:
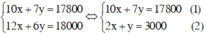
Từ (2) rút ra được y = 3000 – 2x, thay vào (1) ta được :
10x + 7.(3000 – 2x) = 17800
⇔ 10x + 21000 – 14x = 17800
⇔ 4x = 3200 ⇔ x = 800 (thỏa mãn)
Thay x = 800 vào y = 3000 – 2x ta được y = 1400 (thỏa mãn)
Vậy giá tiền một quả quýt là 800đ và giá tiền một quả cam là 1400đ.
Dì Ly mang 100000 đồng đi mua cam. Dì mua 8 quả cam, trung bình mỗi quả nặng 0,25 kg. Biết mỗi kg cam là 35000 đồng. Tính số tiền dì Ly còn lại sau khi mua cam\(\left[{}\begin{matrix}&&&&\\&&&&\end{matrix}\right.\begin{matrix}\\\\\\\end{matrix}\right.\)

Đặt số cam là x, quýt là y (x,y>0)
=>\(\left\{{}\begin{matrix}\dfrac{2x}{5}+\dfrac{4y}{7}=140\\\dfrac{5x}{6}+\dfrac{9y}{14}=215\end{matrix}\right.\)
bấm máy giải hệ
=>\(\left\{{}\begin{matrix}x=150\\y=140\end{matrix}\right.\)

Gọi x (đồng) là giá tiền một quả quýt và y (đồng) là giá tiền một quả cam. Điều kiện
x > 0, y > 0 ta có hệ phương trình:
\(10x+7y=17800\)
\(12x+6y=18000\)
<=> Hệ phương trình \(10x+7y=17800\)
\(2x+y=3000\)
<=> Hệ phương trình 2x + y = 3000
2y = 28000
<=> x= 800 và y = 1400.
Trả lời: Giá tiền một quả quýt: 800 đồng, một quả cam 1400 đông
Vân:10 quả quýt,7 quả cam=17 800 đồng
Lan:12 quả quýt,6 quả cam=18 000 đồng
Nếu cả số quýt và cam của vân mua gấp lên 2 lần thì đc
20 quýt+14 cam=35 600 đồng
-12 quýt+6 cam=18 000đông
=8 quýt+8 cam=17 600 đồng
giá tiền 1 quả quýt là: 17 600 -8=17 592 đồng
giá tiền1 quả cam là: 17 6 00- 17 592 =8


Để cam nhiều hơn thì sẽ có 3 th:
TH1: 2 cam, 1 mận, 1 xoài
=>Có \(C^2_8\cdot5\cdot4=560\)
TH2: 3 cam, 1 xoài
=>Có \(C^3_8\cdot4=224\left(cách\right)\)
TH3: 3 cam, 1 mận
=>Có \(C^3_8\cdot5=280\left(cách\right)\)
=>n(A)=280+224+560=1064
\(n\left(\Omega\right)=C^4_{17}=2380\)
=>P(A)=1064/2380=38/85