Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\: \: \)\(\Rightarrow\dfrac{1}{20}=\dfrac{1}{40}+\dfrac{1}{d'}\:\)
\(\Rightarrow\dfrac{1}{d'}=\dfrac{1}{20}-\dfrac{1}{40}\)
\(\Rightarrow d'=40\) (cm)
c) Chiều cao của ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\) \(\Rightarrow\dfrac{10}{h'}=\dfrac{40}{40}\)
\(\Rightarrow h'=10\) (cm)

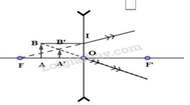
Xét tam giác OAB và tam giác OA’B’ có góc A= góc A' = 90 độ
góc O chung
Vậy tam giác OAB đồng dạng tam giác OA'B' , ta có tỉ số đồng dạng:
\(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\Rightarrow\dfrac{d}{d'}=\dfrac{h}{h'}\)
Xét tam giác IOF’ và tam giác B’A’F’ có góc O = góc A' = 90 độ ,
góc F' chung
Nên ∆IOF’~ ∆B’A’F’
Ta có tỉ số đồng dạng:
\(\dfrac{OI}{B'A'}=\dfrac{F'O}{F'A'}\Rightarrow\dfrac{AB}{A'B'}=\dfrac{F'O}{F'O-A'O}\Leftrightarrow\dfrac{h}{h'}=\dfrac{f}{f-d'}\)
Sử dụng hai công thức đồng dạng và thay số ta có:
\(\dfrac{d}{d'}=\dfrac{h}{h'}=\dfrac{f}{f-d'}\Rightarrow\dfrac{10}{d'}=\dfrac{15}{15-d'}\Rightarrow-10.d'+10.15=15d'\)
\(\Rightarrow25d'=25.10\Rightarrow d'=6cm\)
\(\dfrac{d}{d'}=\dfrac{h}{h'}\Rightarrow\dfrac{10}{6}=\dfrac{5}{h'}\Rightarrow h'=3cm\)
Vậy ảnh cách thấu kính 6 cm và cao 3 cm
Ngu z , phải là tam giác IOF đồng dạng với tam giác B'A'F chứ má ơi

Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{30}+\dfrac{1}{d'}\)
\(\Rightarrow d'=15cm\)