Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khe hở là chung cho cả hai đầu thanh đối diện nhau nên khe hở phải đủ rộng để mỗi đầu nở ra \(\frac{\triangle l}{2}\) , tức là hai đầu sẽ là \(\triangle l\).
Ta có : \(\triangle l=l_0a\triangle t=10.11,4.10^{-6}\left(50-20\right)=3,42.10^{-3}\)( m) = 3,42 mm
Vậy phải để hở một đoạn \(\triangle l=3,42\)mm giữa hai đầu thanh.
Thôi nhá
Đừng tử hỏi tự trả lời nữa
Không ai cạnh tranh đc đâu

Ta có Δ l = α . l 0 ( t − t 0 ) = 12.10 − 6 .10. ( 60 − 20 ) Δ l = 4 , 8.10 − 3 ( m )

* Cách 1 :
Khoảng cách giữa 2 thanh ray liên tiếp nhau chính là độ nở dài của mỗi thanh .
Ta có : △l = l0a . △t
→ Độ biến dạng thiên nhiệt độ △t :
△t = \(\frac{\triangle l}{l_0.a}=\frac{4,5.10^{-3}}{12,5.12.10^{-8}}=0,03.10^3=30^oC\)
Nhiệt độ môi trường lớn nhất để thanh ray không bị cong :
tmax = △t + t = 15oC + 30oC = 45oC
Đáp số 450C
* Cách 2 :
Để thanh ray không bị cong khi nhiệt độ tăng thì độ tăng chiều dài của thanh phải bằng khoảng cách giữa hai đầu thanh ray.
∆l = l2 - l1 = l1α(t2 – t1)
=> t2 = tmax = + t1=
+ 15
=> tmax = 45o

Để thanh ray không bị cong khi nhiệt độ tăng thì độ tăng chiều dài của thanh phải bằng khoảng cách giữa hai đầu thanh ray.
∆l = l2 - l1 = l1α(t2 – t1)
=> t2 = tmax = + t1=
+ 15
=> tmax = 45o.
Khoảng cách giữa 2 thanh ray liên tiếp nhau chính là độ nở dài của mỗi thanh .
Ta có : \(\triangle\)l = l0a . \(\triangle\)t
→ Độ biến dạng thiên nhiệt độ \(\triangle\)t :
\(\triangle t=\frac{\triangle l}{l_0.a}=\frac{4,5.10^{-3}}{12,5.12.10^{-6}}=0,03.10^3=30\) độ C
Nhiệt độ môi trường lớn nhất để thanh ray không bị cong :
tmax = \(\triangle\)t + t = 15 độ C + 30 độ C = 45 độ C
Đáp số 45 độ C

Để thanh ray không bị cong khi nhiệt độ tăng thì độ tăng chiều dài của thanh phải bằng khoảng cách giữa hai đầu thanh ray.
∆l = l2 - l1 = l1α(t2 – t1)
=> t2 = tmax = △lαl1△lαl1+ t1= 4,5.10−312.10−6..12,54,5.10−312.10−6..12,5 + 15
=> tmax = 45o.

Vì các thanh ray được đặt nối tiếp nhau, ở cả hai đầu thanh ray đều có khe hở và các thanh ray nở cả về hai đầu nên khe hở phải có độ rộng h tương ứng với độ nở dài của một thanh ray khi nhiệt độ tăng từ 25 ° C lên 60 ° C Áp dụng công thức: 1 = 1 0 ( 1 + α t )
![]()
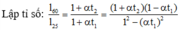
![]()
![]()
![]()

![]()

Đáp án: C
Vì các thanh ray được đặt nối tiếp nhau, ở cả hai đầu thanh ray đều có khe hở và các thanh ray nở cả về hai đầu nên khe hở phải có độ rộng h tương ứng với độ nở dài của một thanh ray khi nhiệt độ tăng từ 25 oC lên 60 oC.
Áp dụng công thức: l = l 0 ( l + α t ) (l0 là chiều dài ở 0 oC)
Ở 250C : l 25 = l 0 ( l + t 1 α ) và ở 600C : l 60 = l 0 ( l + t 2 α )
Lập tỉ số:

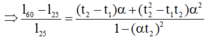
Thép làm thanh ray có α = 11 , 4 . 10 - 6 K - 1 n ê n α 2 ≪ 1 có thể bỏ qua.
Khi đó:
![]()
Thay số:
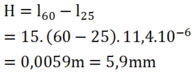

Chọn A
Vì các thanh ray được đặt nối tiếp nhau, ở cả hai đầu thanh ray đều có khe hở và các thanh ray nở cả về hai đầu nên khe hở phải có độ rộng h tương ứng với độ nở dài của một thanh ray khi nhiệt độ tăng từ 25 o C lên 60 o C
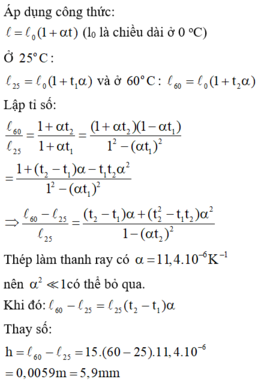
Ta có: l 2 = l 1 ( 1 + α Δ t ) ⇒ Δ l = l 2 − l 1 = l 1 α Δ t
Với l 1 = 10 m , Δ t = 50 − 20 = 30 0 C , α = 12.10 − 6 K − 1
⇒ Δ l = 12.12.10 − 6 . ( 50 − 20 ) = 3 . 10 − 3 m Δ l = 3 , 6 m m
Phải để hở đầu thanh ray 3,6mm.