Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Giữa A và B có 5 đỉnh sóng với A, B cũng là đỉnh sóng
Chuẩn hóa λ = 1
Ta có:
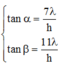
= tan ∠ C
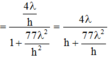
→ Từ biểu thức trên, ta thấy rằng góc ∠ A C B lớn nhất khi
Gọi M là một điểm trên AC, để M ngược pha với nguồn thì
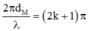
Với khoảng giá trị của d M , tính về phía C từ đường vuông góc của O lên AC:
kết hợp với chức năng Mode → 7 ta tìm được 4 vị trí
Tương tự như vậy ta xét đoạn về phía A: 
ta cũng tìm được 2 vị trí.
→ Trên AC có 6 vị trí
Đáp án C
Để đơn giản, ta chọn λ = 1 → A B = 6 , 6
Để một điểm trên A C cực đại và cùng pha với nguồn thì d 1 + d 2 = k d 1 + d 2 = n ≥ A B = 6 , 6 . Trong đó n và k có độ lớn cùng chẵn hoặc lẻ
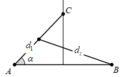
Mặc khác để khoảng cách A C là ngắn nhất thì cos α = A B 2 + d 1 2 − d 2 2 2 A B . d 1 phải lớn nhất
Ta để ý rằng khi xảy ra cực đại thì mỗi bên trung trực của A B có 6 dãy cực đại ứng với k = 1 , ± 2..... ± 6 . Với mỗi giá trị của k ta tìm được cặp giá trị d 1 , d 2
→ Thử các giá trị của k , nhận thấy cos α lớn nhất khi k = 1 và d 1 = 3 d 2 = 4
→ h min = A B 2 tan α ≈ 1 , 3757
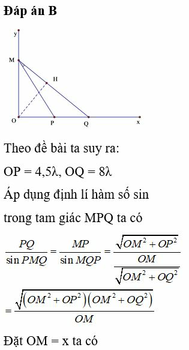
Đáp án B
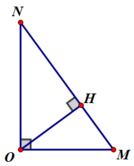
Kẻ OH vuông góc với MB. Áp dụng hệ thức lượng:
Để dao động ngược pha với O thì độ lệch pha phải là số lẻ lần π . Như vậy ta có :
+ Trên NH : độ lệch pha từ 13,32 π đến 24 π , như vậy có các điểm ngược pha là 15, 17, 19, 21, 23.
+ Trên HM : độ lệch pha từ 13,32 π đến 16 π , vậy có điểm ngược pha 15.
Vậy trên MN tổng cộng có 6 điểm ngược pha O.
Đáp án A
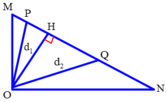
Xét tam giác MON vuông tại O và OH là đường cao nên ta có:
Gọi P là điểm nằm trên đoạn MH, cách nguồn một đoạn d1 và dao động ngược pha với nguồn, ta có:
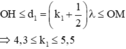
=> k1 = 5 có một điểm dao động ngược pha với nguồn trên đoạn MH.
Gọi Q là điểm nằm trên đoạn NH, cách nguồn một đoạn d2 và dao động ngược pha với nguồn, ta có:
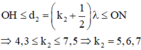
=> có 3 điểm dao động ngược pha với nguồn O trên đoạn NH.
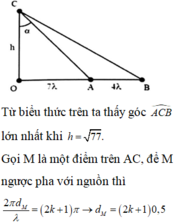
Chọn đáp án C
Giữa A và B có 5 đỉnh sóng với A, B cũng là đỉnh sóng → A B = 4 λ . Chuẩn hóa λ = 1 .
Ta có:
Từ biểu thức trên ta thấy góc A C B ^ lớn nhất khi h = 77 .
Gọi M là một điểm trên AC, để M ngược pha với nguồn thì
Với khoảng giá trị tính về phía C từ đường vuông góc của O lên AC:
kết hợp với chức năng Mode → 7 ta tìm được 4 vị trí.
Tương tự như vậy, ta xét đoạn về phía A: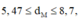
ta tìm được 2 vị trí
→ Trên AC có 6 vị trí.