Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Hai điểm gần nhau nhất trên cùng 1 phương truyền sóng dao động cùng pha cách nhau 1 bước sóng.
Áp dụng công thức tính bước sóng λ = v.T = v/f = 100/25 = 4 cm.

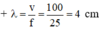
+ Hai điểm gần nhau nhất dao động ngược pha ứng với khoảng cách
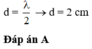

uM=Acoss(wt-2pi d/ lamda) = A cos (wt - 2pi/3)
Khi t=T/3 thay vào ta đc: uM = A cos (2pi/3 - 2pi/2) = A = 5
Pt của M: uM = 5 cos (wt - 2pi/3)

Đáp án B
Hai điểm gần nhau nhất trên cùng một phương truyền sóng dao động ngược pha cách nhau λ/2 => λ = 6.2 = 12 cm

Đáp án B
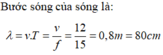
B và C cách nhau 40 cm bằng nửa bước sóng nên chúng dao động ngược pha nhau.
Mà đây là sóng dọc nên khi dao động chúng gần nhau nhất thì khoảng cách giữa chúng là : 40-(2.4)=32cm

Ta thấy trên nửa đường thẳng thẳng kẻ từ A và vuông góc với AB có 4 điểm theo thứ tự M, N, P, Q dao động với biên độ cực đại, nên trên AB có 9 điểm dao động với biên độ cực đai với - 4 ≤ k ≤ 4 ( d2 – d1 = kλ)
A B x M N P Q
Cực đại tại M, N, P, Q ứng với k = 1; 2; 3; 4
Đặt AB = a
Tại C trên Ax là điểm dao động với biên độ cực đại:
CB – CA = kλ (*)
CB2 – CA2 = a2 → (CB + CA) (CB – CA) = a2
CB + CA = \(\dfrac{a^2}{k.\lambda}\)(**)
Từ (*) và (**) suy ra \(CA=\dfrac{a^2}{2k.\lambda}-\dfrac{k}{2}\lambda\)
Tại M: ứng với k = 1: MA = \(\dfrac{a^2}{2\lambda}\)- 0,5λ (1)
Tại N: ứng với k = 2: NA = \(\dfrac{a^2}{4\lambda}\)- λ (2)
Tại P: ứng với k = 3: PA = \(\dfrac{a^2}{6\lambda}\) - 1,5 λ (3)
Tại Q: ứng với k = 4: QA = \(\dfrac{a^2}{8\lambda}\) - 2 λ (4)
Lấy (1) – (2) : MN = MA – NA = \(\dfrac{a^2}{4\lambda}\) + 0,5λ = 22,25 cm (5)
Lấy (2) – (3) : NP = NA – PA = \(\dfrac{a^2}{12\lambda}\) + 0,5λ = 8,75 cm (6)
Lấy (5) - (6) → \(\dfrac{a^2}{\lambda}\) = 81 (cm) và λ = 4 cm .
Thế vào (4) → QA = 2,125 cm.
thầy có thể giải thích e chổ CB-CA= Klamda . Với tại s CB= K/2 lamda k thầy?

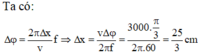

Chọn D.
Bước sóng λ = v/f = 4cm
Hai điểm gần nhau nhất dao động cùng pha cách nhau 1 bước sóng = 4cm