Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
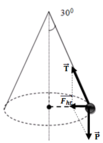
Tổng hợp lực của trọng lực và lực căng dây đóng vai trò là lực hướng tâm:
→ Fht/P = tan30o → Fht = 0,5.9,8.tan30o = 2,83 N
Quả cầu chuyển động theo quỹ đạo tròn với bán kính:
r = ℓsin30o = 0,5.sin30o = 0,25 m.
Mặt khác: → v = 1,19 m/s.

Chọn A.
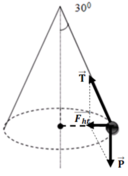
Tổng hợp lực của trọng lực và lực căng dây đóng vai trò là lực hướng tâm:
→ Fht/P = tan 30 o
→ Fht = 0,5.9,8. tan 30 o = 2,83 N
Quả cầu chuyển động theo quỹ đạo tròn với bán kính:
r = l sin 30 o ° = 0,5. sin 30 o ° = 0,25 m.
Mặt khác:
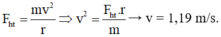

Đáp án A
Tổng hợp lực của trọng lực và lực căng dây đóng vai trò là lực hướng tâm.

Quả cầu chuyển động theo quỹ đạo tròn với bán kính
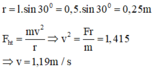

Chọn đáp án A
Tổng hợp lực của trọng lực và lực căng dây đóng vai trò là lực hướng tâm:
→ Fht/P = tan30o
→ Fht = 0,5.9,8.tan30o = 2,83 N
Quả cầu chuyển động theo quỹ đạo tròn với bán kính:
r = ℓsin30o = 0,5.sin30o = 0,25 m
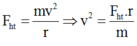
→ v = 1,19 m/s.
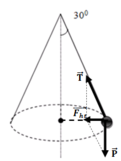

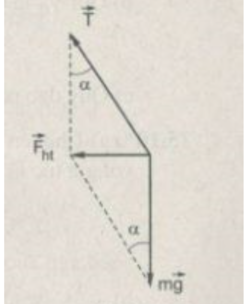
Từ hình vẽ ta có
F h t = mgtanα
Mà F h t = m v 2 /r = m v 2 /1.sin α
Suy ra m v 2 /1.sin α = mgtan α
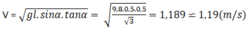

T P F ht
\(tan\alpha=\dfrac{F_{ht}}{P}\)
Fht\(=\dfrac{v^2}{R}.m\)
khoảng cách từ quả cầu tới trục quay là R
\(sin\alpha\dfrac{R}{l}\Rightarrow R=l.sin\alpha\)
P=m.g
kết hợp tất cả điều trên
\(\Rightarrow v\approx1,2\)m/s
r 30 0,5m
Tổng hợp lực của trong lực và lực căng dây đóng vai trò là lực hướng tâm \(\Rightarrow\dfrac{F_{ht}}{P}=tan30^o\Rightarrow F_{ht}=m.g.tan30^o=0,5.10.\dfrac{\sqrt{3}}{3}=2,89N\)
Qủa cầu chuyển động theo quỹ đạo tròn với bán kính
\(r=l.sin30^o=0,5.sin30^o=0,25m\)
\(F_{ht}=\dfrac{m.v^2}{r}\Rightarrow v=\sqrt{\dfrac{F_{ht}.r}{m}}=\sqrt{\dfrac{2,89.0,25}{0,5}}\approx1,2\) (m/s)

Các lực tác dụng lên vật như hình 53.
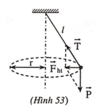
Lực hướng tâm là hợp lực của trọng lực P → và lực căng dây T → . Dùng định luật II Niu-tơn thu được số vòng quay trong một giây:
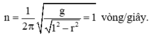

Ta có: \(F_{ht}=mg+T\)
\(\Leftrightarrow T^2=\left(mg\right)^2+F_{ht}^2\left(Pytago\right)\)
\(\Leftrightarrow T^2=F_{ht}^2+\left(mg\right)^2=\left(\dfrac{mv^2}{R}\right)+\left(mg\right)^2\)
\(\Rightarrow m=\dfrac{T}{\sqrt{g^2+\dfrac{v^4}{R^2}}}\approx0,8\left(kg\right)\)

T P F ht
T=\(\dfrac{P}{cos\alpha}\)=\(\dfrac{\sqrt{2}}{4}N\)
tan\(\alpha=\dfrac{F_{ht}}{P}\)=\(\dfrac{\omega^2.sin\alpha.l.m}{m.g}\)\(\Rightarrow\)\(\omega\approx5,318\) (rad/s)
T=\(\dfrac{2\pi}{\omega}\)\(\approx\)1,18s
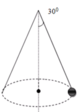
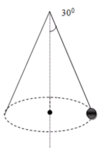
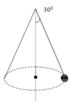
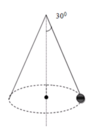
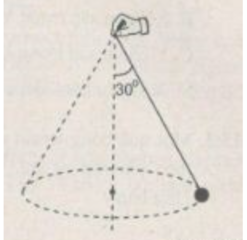
trục quay L P T F
khoảng cách từ vật đến trục quay là R
\(sin\alpha=\dfrac{R}{l}\)
\(\Rightarrow R=l.sin\alpha\)
theo hình ta có
\(tan\alpha=\dfrac{F_{ht}}{P}\)
\(\Leftrightarrow tan\alpha=\dfrac{m.\dfrac{v^2}{R}}{m.g}\) kết hợp với R=sin\(\alpha\).l
\(\Rightarrow v\approx1,2\)m/s2