Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Vẽ đồ thị hàm số \(y = x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{1} = - 3\) ta được điểm \(B\left( { - 3;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = x + 3\) là đường thẳng đi qua hai điểm \(A\) và \(B\).
- Vẽ đồ thị hàm số \(y = - x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{{ - 1}} = 3\) ta được điểm \(C\left( {3;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = - x + 3\) là đường thẳng đi qua hai điểm \(A\) và \(C\).
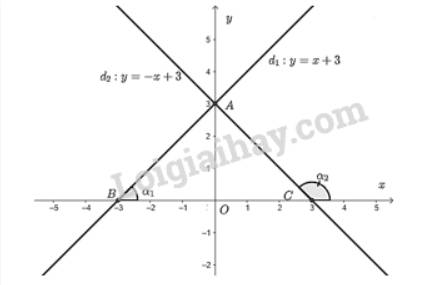
Từ đồ thị ta thấy giao điểm của hai đường thẳng là \(A\left( {0;3} \right)\).
Đường thẳng \({d_1}\) cắt trục \(Ox\) tại \(B\left( { - 3;0} \right)\).
Đường thẳng \({d_2}\) cắt trục \(Oy\) tại \(C\left( {3;0} \right)\).

Gọi \({\alpha _1};{\alpha _2}\) lần lượt là 2 góc tạo bởi đường thẳng \({d_1};{d_2}\) với \(Ox\).
Dùng thước đo độ ta kiểm tra được\({\alpha _1} = 45^\circ ;{\alpha _2} = 135^\circ \).

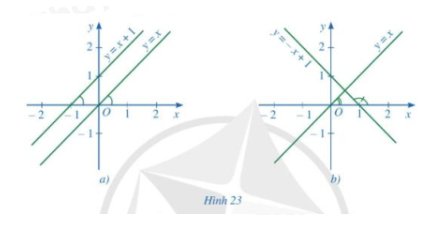
a) Hệ số góc của đường thẳng y = x là 1
Hệ số góc của đường thẳng y = x + 1 là 1
Hai đường thẳng y = x và y = x + 1 song song với nhau
b) Hệ số góc của đường thẳng y x là 1
Hệ số góc của đường thẳng y = -x + 1 là -1
Hai đường thẳng y = x và y = -x + 1 cắt nhau.

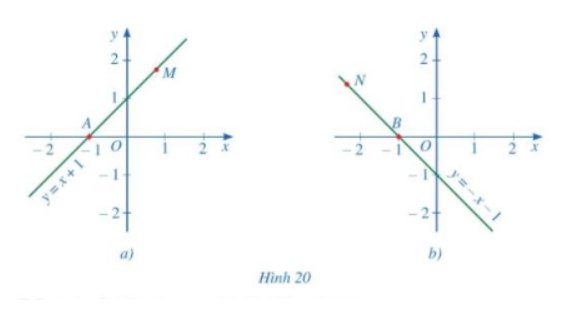
a) Tung độ của điểm M mang dấu dương.
Tung độ của điểm N mang dấu dương.
b) Góc tạo bởi hai tia Ax và AM là góc MAO
c) Góc tạo bởi 2 tia Bx và BN là góc NBO

Nhìn câu b thấy "chạy chạy" chắc hẳn là độ lầy của câu này cũng siêu cao :v, đang ngu não chờ tối tối làm thử :v
P/s : up lên CHH luôn cho các thánh theo dõi :V
mấy bạn làm nêu hộ hướng ch/minh giùm cái vs nha 8.8
cảm ưn nhièu

a) Đường thẳng \(d:y = 2x\) và \(d':y = x\) đều có dạng \(y = ax\) nên giao điểm của hai đường thẳng là \(O\left( {0;0} \right)\) (cả hai đường thẳng đều đi qua điểm \(O\left( {0;0} \right)\).
b)
- Hệ số góc của đường thẳng \(d:y = 2x\) là\(a = 2\).
- Hệ số góc của đường thẳng \(d':y = x\) là\(a = 1\).
Hai đường thẳng có hệ số góc khác nhau thì cắt nhau.
c) Vì \(d\) và \(d''\) cắt nhau nên chúng không thể song song với nhau hoặc trùng nhau. Do đó, hệ số góc của \(d\) và \(d''\) phải khác nhau. Khi đó, hệ số góc của \(d''\) khác 2.

Vì \(Ox \bot Oy\) tại \(O\)nên tam giác \(AOB\) và tam giác \(AOC\) đều vuông tại \(O\).
Ta có: \(OA = 3;OB = 3;OC = 3\)
\(BC = OB + OC = 3 + 3 = 6\).
Áp dụng định lí Py – ta – go cho tam giác \(AOB\) ta có:
\(O{A^2} + O{B^2} = A{B^2}\)
\( \Leftrightarrow {3^2} + {3^2} = A{B^2}\)
\( \Leftrightarrow A{B^2} = 9 + 9 = 18\)
\( \Leftrightarrow AB = \sqrt {18} = 3\sqrt 2 \)
Áp dụng định lí Py – ta – go cho tam giác \(AOC\) ta có:
\(O{A^2} + O{C^2} = A{C^2}\)
\( \Leftrightarrow {3^2} + {3^2} = A{C^2}\)
\( \Leftrightarrow A{C^2} = 9 + 9 = 18\)
\( \Leftrightarrow AC = \sqrt {18} = 3\sqrt 2 \)
Chu vi tam giác \(ABC\) là:
\(C = AB + AC + BC = 3\sqrt 2 + 3\sqrt 2 + 6 = 6 + 6\sqrt 2 \) (đơn vị độ dài)
Vì \(Ox \bot Oy\) nên \(OA\) vuông góc với \(BC\) tại \(O\). Do đó, \(OA\) là đường cao tam giác \(ABC\) ứng với cạnh \(BC\).
Diện tích tam giác \(ABC\) là:
\(S = \dfrac{1}{2}OA.BC = \dfrac{1}{2}.3.6 = 9\) (đơn vị diện tích)
Vậy chu vi tam giác \(ABC\) là \(6 + 6\sqrt 2 \) đơn vị độ dài và diện tích tam giác \(ABC\) là 9 đơn vị diện tích.

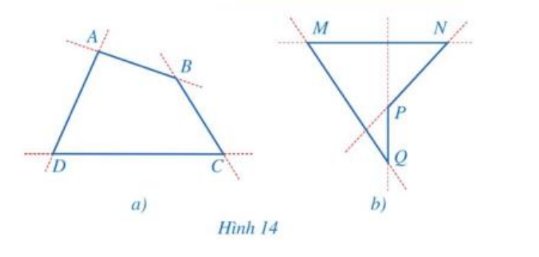
Hình 14a: Tứ giác ABCD luôn nằm về 1 phía của 1 cạnh bất kì.
Hình 14b: Tứ giác MNPQ nằm về 2 phía của đường thẳng chứa cạnh PQ, cạnh NP

a) Gọi hàm số bậc nhất của đường thẳng d là y = ax + b (a\( \ne \)0)
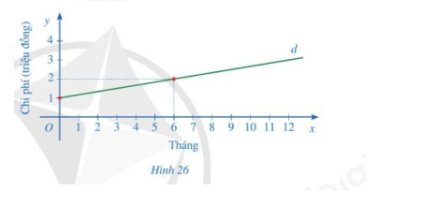
Từ hình 26, ta thấy đường thẳng d đi qua hai điểm (0; 1) và (6; 2)
Thay tọa độ điểm (0; 1) vào hàm số y = ax + b ta được:
1 = a. 0 + b suy ra b = 1
Hàm số bậc nhất là y = ax + 1 (a\( \ne \)0) (1)
Vì đường thẳng d đi qua điểm (6; 2) nên thay tọa độ điểm (6; 2) vào hàm số (1) ta được là:
2 = a. 6 + 1 suy ra \(a = \dfrac{1}{6}\)
Vậy hàm số của đường thẳng d là \(y = \dfrac{1}{6}x + 1\)
b) Giao điểm của đường thẳng d với trục tung là 1 trong tình huống này có nghĩa là người dùng phải trả khoản phí bạn đầu là 1 triệu đồng
c) Tổng chi phí mà gia đình phải trả khi sử dụng dịch vụ truyền hình với thời gian 12 tháng là ta thay x = 12 vào hàm số \(y = \dfrac{1}{6}x + 1\)
Khi đó: \(y = \dfrac{1}{6}.12 + 1 = 3\)
Tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng là 3 triệu đồng.


a) Quan sát hình 24, ta thấy:
Tung độ giao điểm của hai đường thẳng \({d_1},{d_2}\) đều bằng 2.
Nhận xét: Hai chuyển động đều có cùng tốc độ ban đầu là 2m/s.
b) Trong 2 đường thẳng \({d_1},{d_2}\) đường thẳng d2 có hệ số góc lớn hơn.
c) Từ giây thứ nhất trở đi, vật thứ hai có tốc độ lớn hơn vì đường thẳng d2 cao hơn đường thẳng d1 từ giây thứ nhất.