Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Công mà điện trường giữa anôt và catôt của ống Rơn-ghen sinh ra khi êlectron bay từ catôt đến anôt bằng đô tăng động năng của êlectron :
- e U A K = W s - W t = m v 2 / 2 - 0 ⇒ m v 2 / 2 = e U K
⇒ λ m i n = h / e U A K = 6 , 2 . 10 - 9 m
Năng lượng bức xạ của ống Ronghen trong 1 giây là
Năng lượng tiêu thụ của ống Ronghen trong 1 giây chính là nhiệt lượng tạo ra nên:
Đáp án B
Đáp án B
Số electron qua ống trong 1s là :
Động năng 1 electron khi đập vào A :
Tổng động năng đập vào A/1s là :
Năng lượng nhiệt do nước hấp thụ là :
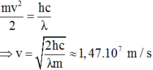
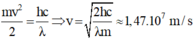
Chọn đáp án D