Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chọn hệ trục tọa độ Oxy với gốc tọa độ tại tâm đáy nhà vòm, trục tung thẳng đứng

Nhà vòm có dạng elip nên có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (với a,b>0)
Ta có chiều cao 8 m nên \(OA = b = 8\), chiều rộng của vòm là 20 m, suy ra \(BC = 2a = 20 \Rightarrow a = 10\).
Suy ra, phương trình miêu tả hình dáng nhà vòm là \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)
b) Điểm đó cách chân tưởng 5 m tương ứng cách tâm 5 m (vì từ tâm vòm đến tưởng là 10 m)
Thay \(x = 5\) vào phương trình \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\), ta tìm được \(y = 4\sqrt 3 \)
Vậy khoảng cách phương thẳng đứng từ một điểm cách chân tường 5 m đến nóc nhà vòm là \(4\sqrt 3\) m

75 cm trên bản vẽ ứng với 2,5 đơn vị trên mặt phẳng tọa độ.
Gọi M là điểm trên vòm ô thoáng, có hoành độ 2,5 và tung độ là h.
M thuộc elip nên \(\frac{{2,{5^2}}}{{16}} + \frac{{{h^2}}}{4} = 1\)
\(\Leftrightarrow h = \sqrt {4.\left( {1 - \frac{{2,{5^2}}}{{16}}} \right)} = \frac{{\sqrt {39} }}{4} \approx 1,56\)
Vậy độ cao h trên thực tế là: \(h = 1,56.30 = 46,8\) cm

Gọi khoảng cách từ tâm đối xứng đến đáy tháp là z
Suy ra khoảng cách từ tâm đối xứng đến nóc tháp là \(\frac{2}{3}z\)
Ta có \(z + \frac{2}{3}z = 150 \Rightarrow z = 90\)
Thay \(y = 90\) vào phương trình \(\frac{{{x^2}}}{{{{28}^2}}} - \frac{{{y^2}}}{{{{42}^2}}} = 1\) ta tìm được \(x = 4\sqrt {274} \)
Thay \(y = 60\) vào phương trình \(\frac{{{x^2}}}{{{{28}^2}}} - \frac{{{y^2}}}{{{{42}^2}}} = 1\) ta tìm được \(x = 4\sqrt {149} \)
Vậy bán kính đường tròn nóc và bán kính đường tròn đáy của tháp lần lượt là \(4\sqrt {149} \) m và \(4\sqrt {274} \)m

Gọi khoảng cách từ tâm đối xứng đến đỉnh tháp là z
Suy ra khoảng cách từ tâm đối xứng đến đáy tháp là 2z
Ta có \(z + 2z = 120 \Rightarrow z = 40\)
Thay \(y = 40\) vào phương trình \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) ta tìm được \(x = 27\sqrt 2 \)
Thay \(y = 80\) vào phương trình \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) ta tìm được \(x = 27\sqrt 5 \)
Vậy bán kính đường tròn nóc và bán kính đường tròn đáy của tháp lần lượt là \(27\sqrt 2 \) và \(27\sqrt 5 \)

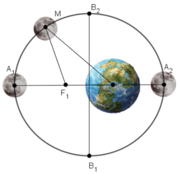
Theo đề bài có:
Độ dài trục lớn của elip bằng 769266km ⇒ A1A2 = 2a = 769266 ⇒ a = 384633
Độ dài trục nhỏ của elip bằng 768106km ⇒ B1B2 = 2b = 768106 ⇒ b = 384053
⇒ c2 = a2 – b2 = 445837880 ⇒ c ≈ 21115
⇒ F1F2 = 2c = 42230
⇒ A1F1 = A2F2 = (A1A2 – F1F2)/2 = 363518
+ Trái Đất gần Mặt Trăng nhất khi Mặt Trăng ở điểm A2
⇒ khoảng cách ngắn nhất giữa Trái Đất và Mặt Trăng bằng A2F2 = 363518 km
+ Trái Đất xa Mặt Trăng nhất khi Mặt Trăng ở điểm A1
⇒ khoảng cách xa nhất giữa Trái Đất và Mặt Trăng bằng:
A1F2 = A1F1 + F1F2 = 405748 km.

a) \(\left(E\right):\dfrac{x^2}{100}+\dfrac{y^2}{36}=1\)
b) \(\left(E\right):\dfrac{x^2}{169}+\dfrac{y^2}{25}=1\)

\(F_1\left(-2\sqrt{2};0\right);F_2\left(2\sqrt{2};0\right)\)
Gọi \(M\left(x;y\right)\Rightarrow\frac{x^2}{9}+\frac{y^2}{1}=1\) (1) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{F_1M}=\left(x+2\sqrt{2};y\right)\\\overrightarrow{F_2M}=\left(x-2\sqrt{2};y\right)\end{matrix}\right.\)
Do \(\widehat{F_1MF_2}=90^0\Rightarrow F_1M\perp F_2M\Rightarrow\overrightarrow{F_1M}.\overrightarrow{F_2M}=0\)
\(\Rightarrow\left(x-2\sqrt{2}\right)\left(x+2\sqrt{2}\right)+y^2=0\Rightarrow x^2+y^2=8\) (2)
Từ (1) và (2) có hệ: \(\left\{{}\begin{matrix}\frac{1}{9}x^2+y^2=1\\x^2+y^2=8\end{matrix}\right.\) \(\Rightarrow x^2=\frac{63}{8}\Rightarrow x=\frac{3\sqrt{14}}{4}\)
Câu 2:
\(F_1F_2=24=2c\Rightarrow c=12\)
\(2a=26\Rightarrow a=13\)
\(\Rightarrow b^2=a^2-c^2=13^2-12^2=25\Rightarrow b=5\)
Vậy xưởng cao 5m





