Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

có nhiều cách đi cho cùng một khoảng thời gian. nên mình chỉ ra 1 trường hợp thôi nhé :
Cách đi sẽ đi như sau
| người đi | thời gian |
| AB đi qua | 2 phút |
| A quay về | 1 phút |
| CD đi qua | 10 phút |
| B quay về | 2 phút |
| AB đi qua | 2 phút |
Vậy cộng lại thời gian ngắn nhất có thể là : 17 phút

Bước 1: Gọi số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất lần lượt là \(x\) và \(y\) \(\left( {x,y \in \mathbb{N}} \right)\).
+ Theo giả thiết, thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất nên \(0 \le x \le 200\)
và 240 chiếc mũ kiểu thứ hai nên ta có \(0 \le y \le 240\)
+ Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc
=> Thời gian làm \(1\) chiếc mũ kiểu thứ hai là 1/60 (giờ)
=> Thời gian làm \(y\) chiếc kiểu hai là \(\frac{y}{{60}}\left( h \right)\)
+ Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai
=> thời gian làm 1 chiếc mũ kiểu thứ nhất là 2.1/60 = 1/30 (giờ)
=> Thời gian làm \(x\) chiếc kiểu thứ nhất là \(\frac{x}{{30}}\left( h \right)\)
+ Tổng thời gian làm một ngày không quá 8h nên ta có:
\(\frac{x}{{30}} + \frac{y}{{60}} \le 8\)
Bước 2: Lập hệ bất phương trình.
\(\left\{ \begin{array}{l}
0 \le x \le 200\\
0 \le y \le 240\\
\frac{x}{{30}} + \frac{y}{{60}} \le 8
\end{array} \right.\)
Bước 3: Biểu diễn miền nghiệm.
Miền biểu diễn miền nghiệm là phần không bị gạch, đa giác OABCD với O(0;0), A(0; 240), B(120; 240), C(200; 80), D(200; 0).
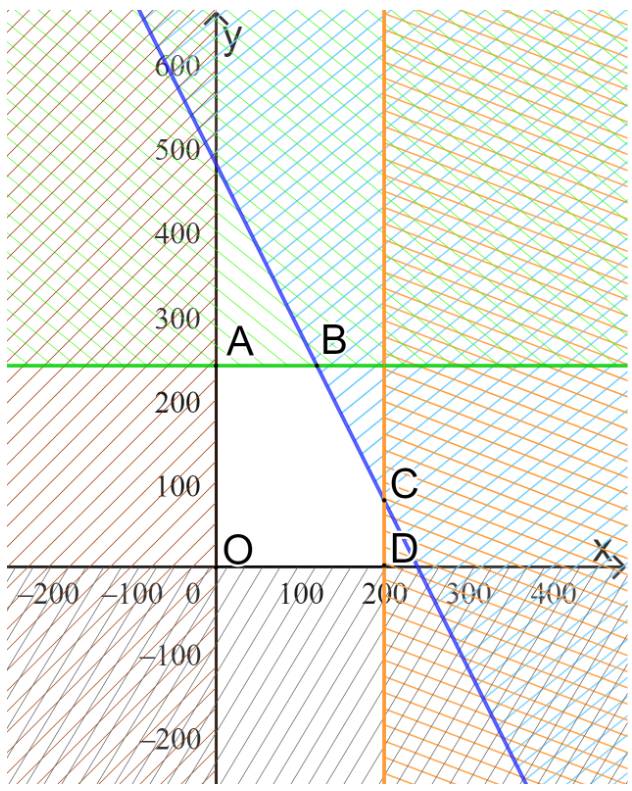
Bước 4: Tìm \(x\) và \(y\) để tiền lãi cao nhất.
Từ miền nghiệm ta thấy tiền lãi cao nhất tại khi điểm \(\left( {x;y} \right)\) là một trong các đỉnh của đa giác OABCD.
\(T = 24x + 15y\)
\(T\left( {0;240} \right) = 15.240 = 3600\) (nghìn đồng)
\(T\left( {120;240} \right) = 24.120+15.240 = 6480\) (nghìn đồng)
\(T\left( {200;80} \right) = 24.200+15.80 = 6000\) (nghìn đồng)
\(T\left( {200;0} \right) = 24.200 = 4800\)(nghìn đồng)
Vậy để tiền lãi thu được nhiều nhất, mỗi ngày xưởng cần sản xuất số mũ kiểu 1 là 120 và mũ kiểu 2 là 240 cái.

Đầu tiên, cứ gọi 2 sợi dây là A và B cho dễ nhé. Muốn giải được câu đố này, bạn phải dựa vào dữ kiện duy nhất được cung cấp: A và B đều cháy hết trong vòng 1 giờ đồng hồ khi đốt cháy một đầu.
Điều này có nghĩa là nếu đốt cháy 2 đầu, sợi dây sẽ cháy trong đúng 30 phút. Và sau khi cháy được một nửa, bạn đốt nốt đầu còn lại, thì khoảng thời gian cho đoạn dây còn lại cháy hết sẽ đúng bằng 15 phút.
Vậy vấn đề bây giờ chỉ là làm cách nào đo được chính xác thời điểm đoạn dây cháy còn một nửa mà thôi.
Dễ quá rồi đúng không: Với dây A, hãy đốt cháy 2 đầu, đồng thời đốt một đầu của dây B.

Đáp án của câu đố kinh điển trên.
Khi dây A cháy hết, dây B sẽ còn 30 phút nữa để cháy. Giờ hãy châm lửa vào đầu còn lại của dây B, và khi B cháy hết, chính xác 45 phút đã trôi qua.
nha hoc24

Phép đo của các nhà thiên văn có sai số tuyệt đối không vượt quá \(\frac{1}{4}\) ngày, có nghĩa là không vượt quá 360 phút. Phép đo của Hùng có sai số tuyệt đối không vượt quá 1 phút. Nếu chỉ so sánh 360 phút và 1 phút thì có thể dẫn đến hiểu rằng phép đo của bạn Hùng chính xác hơn phép đo của các nhà thiên văn. Tuy nhiên, \(\frac{1}{4}\) ngày hay 360 phút là độ chính xác của phép đo một chuyển động trong 365 ngày, còn 1 phút là độ chính xác của phép đo một chuyển động trong 15 phút. So sánh hai tỉ số \(\frac{{\frac{1}{4}}}{{365}} = \frac{1}{{1460}} = 0,0006849...\) và\(\frac{1}{{15}} = 0,0666...\) , ta thấy rằng phép đo của các nhà thiên văn chính xác hơn nhiều.

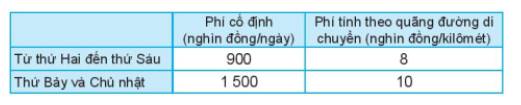
a) Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:
900.5 + 8x = 4 500 + 8x (nghìn đồng).
Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:
1 500.2 + 10y = 3 000 + 10y (nghìn đồng).
Tổng số tiền ông An phải trả cho việc thuê xe trong một tuần là:
4 500 + 8x + 3 000 + 10y = 7 500 + 8x + 10y (nghìn đồng).
Để tổng số tiền ông An phải trả không quá 14 triệu đồng thì
7 500 + 8x + 10y ≤ 14 000
⇔ 8x + 10y ≤ 6 500.
⇔ 4x + 5y ≤ 3 250.
Vậy bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng là 4x + 5y ≤ 3 250.
b)
Vẽ đường thẳng d: 4x + 5y = 3 250 trên mặt phẳng tọa độ.
Lấy gốc tọa độ O(0; 0) và tính 4.0 + 5.0 = 0 < 3 250.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d không chứa gốc tọa độ và cả đường thẳng d (miền không bị gạch kể cả biên)
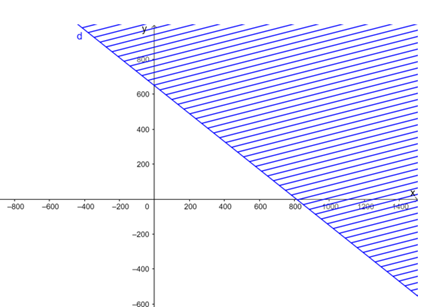
Tham khảo:
a)
Ta có 14 triệu = 14 000 (nghìn đồng)
Phí cố định là: 900.5 + 1500.2 = 7500 (nghìn đồng)
Phí tính theo quãng đường là:
x km trong các ngày từ thứ Hai đến thứ Sáu là 8x (nghìn đồng)
y km trong 2 cuối tuần là 10y (nghìn đồng)
Tổng số tiền ông An phải trả là 8x+10y +7500 (nghìn đồng)
Vì số tiền không quá 14 triệu đồng nên ta có :
\(\begin{array}{l}8x + 10y +7500 \le 14000\\ \Leftrightarrow 4x + 5y \le 3250\end{array}\)
Vậy bất phương trình cần tìm là \(4x + 5y \le 3250\)
b)
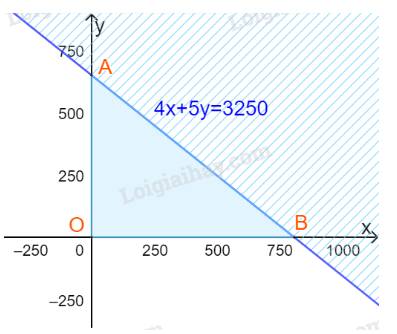
Bước 1: Vẽ đường thẳng \(4x + 5y = 3250\)(nét liền)
Bước 2: Thay tọa độ điểm O(0;0) vào biểu thức 4x+5y ta được:
4.0+5.0=0<3250
=> Điểm O thuộc miền nghiệm
=> Miền nghiệm là nửa mặt phẳng bờ là đường thẳng \(4x + 5y = 3250\) và chứa gốc tọa độ và (x;y) nằm trong miền tam giác OAB kể cả đoạn AB.

Đầu tiên, hãy để cả hai đồng hồ cát cùng chảy
Sau khi đồng hồ 7 phút chảy hết, lật ngược lại và bắt đầu luộc trứng.
Lúc này, chiếc đồng hồ lớn sẽ còn 11 - 7 = 4 phút. Giờ hãy đợi đồng hồ lớn chảy hết cát và lật ngược lại, bạn sẽ có một khoảng thời gian chính xác là 11 + 4 = 15 phút.
1+456= 2+65= 16+90= 57+09= 24-12= 44-24=