Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vân trung tâm sẽ bị dịch chuyển lên phía trên một khoảng là
\(x = \frac{e.(n-1)D}{a}=\frac{10.(1,5-1).2}{0,6}=16,7mm = 1,67cm.\)
Trong thí nghiệm giao thoa ánh sáng khe Y- âng a = 0,6 mm, D = 2 m,λλ = 0,60 μmμm. Đặt ngay sau khe S1 (phía trên) một bản mỏng thủy tinh trong suốt có bề dày 10 μmμm và có chiết suất 1,5. Hỏi vân trung tâm dịch chuyển thế nào?
A.Dịch chuyển lên trên 1,67 mm.
B.Dịch chuyển xuống dưới 1,67 mm.
C Dịch chuyển lên trên 1,67 cm.
D.Dịch chuyển xuống dưới 2,67 mm.

Khi đặt thêm bản mỏng độ dày e vào một trong hai nguồn thì vân trung tâm dời đi một đoạn là
\(x = \frac{e(n-1)D}{a}\)
=> \(e = \frac{ax}{(n-1)D} = \frac{0,5.3}{0,5.1,2}= 2,5 \mu m.\)
Chú ý: khi bấm máy không cần đổi lại đơn vị của các đại lượng.

\(i = \frac{\lambda D}{a} =\frac{0,5. 1}{0,5}=1mm.\)
Số vân sáng trên trường giao thoa L là
\(N_s = 2.[\frac{L}{2i}]+1= 2.2.6+1 = 13.\)
Số vân tối trên trường giao thoa L là
\(N_t = 2.[\frac{L}{2i}+0,5]= 2.7 = 14.\)

Đáp án D
Vì bản thủy tinh đặt trước S 1 nên hệ thống vân trung tâm dịch chuyển về phía S 1 một khoảng:
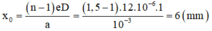

Kính lúp đóng vai trò chính là màn hứng.
Lúc đầu: \(i = \frac{\lambda D}{a}= \frac{2,4}{16}= 0,15mm.(1)\)
\(i' = \frac{\lambda (D+0,3)}{a}= 0,24mm.\)
=> \(\frac{i}{i'}= \frac{D}{D+0,3}= \frac{5}{8}.\)
=> \(D = 0,5m.\)
Bước sóng của bức xạ là \(\lambda = \frac{ai}{D} = \frac{1,8.0,15}{0,5}=0,54 \mu m.\)

Xây dựng từ phần lý thuyết, hiệu đường đi của ánh sáng từ hai khe đến vân tối thứ \(k+1\) là
\(d_2-d_1 = (k+0,5)\lambda.\)
Áp dụng với \(k+1 = 3\) => \(d_2-d_1 = (2+0,5)\lambda = 2,5 \lambda.\)

+ Ban đầu M là vân tối thứ 3 nên: \(x_M=\left(2+\frac{1}{2}\right)\frac{\lambda D}{a}\left(1\right)\)
+ Khi giãm S1S2 một lượng \(\Delta\)a thì M là vân sáng bậc n nên: \(x_M=n\frac{\lambda D}{a-\Delta a}\left(2\right)\)
+ Khi tăng S1S2 một lượng \(\Delta\)a thì M là vân sáng bậc 3n nên: \(x_M=3n\frac{\lambda D}{a+\Delta a}\left(3\right)\)
+ (2) và (3) \(\Rightarrow k\frac{\lambda D}{a-\Delta a}=3k\frac{\lambda d}{a+\Delta a}\Rightarrow\Delta a=\frac{a}{2}\)
+ Khi tăng S1S2 một lượng 2\(\Delta\)a thì M là sáng bậc k nên: \(x_M=k\frac{\lambda D}{a+2\Delta a}=2,5\frac{\lambda D}{a}\left(4\right)\)
+ Từ (1) và (4) \(\Rightarrow\) k = 5. Vậy tại M lúc này là vân sáng bậc 5.

\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

\(\lambda = v/f=20/50=0.4cm.\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{4,8-5,3}{0,4}-\frac{0}{2\pi})|=|2a\cos\frac{-5\pi}{4}|=\sqrt{2}a = 2\sqrt{2}\)
\( u_M = A_M\cos(2\pi ft - \pi\frac{d_2+d_1}{\lambda}+\frac{\varphi_1+\varphi_2}{2})=2\sqrt{2}\cos(40 \pi t - \pi\frac{5,3+4,8}{0,4}+\frac{0}{2}) = 2\sqrt{2}\cos(40 \pi t - \pi\frac{5,3+4,8}{0,4})\\ = 2\sqrt{2}\cos(40 \pi t - 25,25\pi)mm.\)
Khi đặt thêm một bản thủy tinh mỏng trước nguồn S1 thì hệ vân sẽ dịch chuyển về phía S1 một đoạn là
\(x = \frac{e(n-1)D}{a}= \frac{12.0,5.1}{1}=6 mm.\)
Woh. This question is very easy. Does HOC24 have any difficult questions?