Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Bước 1: Biểu diễn diện tích x chiếc ghế và y chiếc bàn.
Diện tích của x chiếc ghế là \(0,5x\left( {{m^2}} \right)\) và y chiếc bàn là \(1,2y\left( {{m^2}} \right)\)
Bước 2: Biểu diễn diện tích lưu thông và cho lớn hơn hoặc bằng 12 \({m^2}\).
Tổng diện tích x chiếc ghế và y chiếc bàn là \(0,5x + 1,2y\left( {{m^2}} \right)\)
Diện tích lưu thông là \(60 - 0,5x - 1,2y\left( {{m^2}} \right)\)
Bất phương trình cần tìm là
\(\begin{array}{l}60 - 0,5x - 1,2y \ge 12\\ \Leftrightarrow 0,5x + 1,2y \le 48\end{array}\)
b)
+) Thay x=10, y=10 ta được
\(0,5.10 + 1,2.10 = 17 \le 48\)
=> (10;10) là nghiệm của bất phương trình
+) Thay x=10, y=20 ta được
\(0,5.10 + 1,2.20 = 29 \le 48\)
=> (10;20) là nghiệm của bất phương trình
+) Thay x=20, y=10 ta được
\(0,5.20 + 1,2.10 = 22 \le 48\)
=> (20;10) là nghiệm của bất phương trình
Chú ý
Ta có thể lấy các giá trị khác để thay vào, nếu thỏa mãn bất phương trình thì đó là nghiệm.

Chọn B
Gọi x; y lần lượt là số cái bánh đậu xanh, bánh dẻo . Khi đó; số tiền lãi là L= 2x+ 1,8 y
Bài toán trở thành tìm số tự nhiên x; y thoả mãn hệ
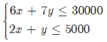 sao cho L= 2x+ 1,8 y lớn nhất.
sao cho L= 2x+ 1,8 y lớn nhất.
Từ đó ta có 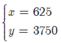 thì L đạt giá trị lớn nhất.
thì L đạt giá trị lớn nhất.
Vậy cần 625 bánh đậu xanh và 3750 bánh dẻo thì lãi lớn nhất.

gọi \(x\times100000\text{ là số tiền vé đã tăng}\)
khi đó \(\hept{\begin{cases}\text{Giá vé khi đó là : }100000\times\left(x+4\right)\\\text{số người trên xe khi đó là : }60-10\times x=10\times\left(6-x\right)\end{cases}}\)
khi đó tổng số tiền bán vé thu được là :
\(100000\times\left(x+4\right)\times10\times\left(6-x\right)=1.000.000\times\left(4+x\right)\times\left(6-x\right)\)
\(\le1.000.000\times\left(\frac{4+x+6-x}{2}\right)^2=25.000.000\)
dấu "=" xảy ra khi \(x+4=6-x\Leftrightarrow x=1\)

Để gắn nhãn cho các ghế ta chọn chọn 1 chữ cái in hoa và 1 số (từ 1 đến 20).
Số cách chọn chữ cái in hoa: 26 cách (tương ứng với 26 chữ)
Số cách chọn số: 20 cách
Vậy số ghế gắn nhãn tối đa là 26.20 = 520 (ghế)

Số cách xếp 3 nam và 3 nữ vào 6 ghế là 6! Cách.
Suy ra: n(Ω)=6!=720n(Ω)=6!=720
a) Ta gọi A là biến cố : “Nam, nữ ngồi xen kẽ nhau”
Ta đánh số ghế như sau:
1 | 2 | 3 | 4 | 5 | 6 |
Trường hợp 1:
+ Nam ngồi ghế số 1, 3, 5 suy ra có 3! cách xếp
+ Nữ ngồi ghế số 2, 4, 6 suy ra có 3! cách xếp
Suy ra trường hợp 1 có 3!.3! = 36 cách xếp
Trường hợp 2:
+ Nữ ngồi ghế số 1, 3, 5 suy ra có 3! cách xếp
+ Nam ngồi ghế số 2, 4, 6 suy ra có 3! cách xếp
Suy ra trường hợp 1 có 3!.3! = 36 cách xếp
Suy ra:
N(A) = 3!.3! + 3!.3! = 36 + 36 = 72 cách xếp.
Vậy P(A)=n(A)n(Ω)=72720=110=0,1P(A)=n(A)n(Ω)=72720=110=0,1
b) Gọi biến cố B: “Ba bạn nam ngồi cạnh nhau”
Xem 3 bạn nam như một phần tử N và N cùng 3 bạn nữ được xem như ngồi vào 4 ghế được đánh số như sau:
1 | 2 | 3 | 4 |
_ Số cách xếp N và 3 nữ vào 4 ghế là 4!
_ Mỗi cách hoán vị 3 nam cho nhau trong cùng một vị trí ta có thêm 3! cách xếp khác nhau.
Suy ra n(B) = 4!.3!=144
Vậy : P(B)=n(B)n(Ω)=144720=15=0,2

Tổng số tiền 2 lần lĩnh là:
480 000 + 540 000 = 1020 000 (đồng)
a) Nếu nhóm đó có 3 người thì trung bình mỗi người làm được:
1020 000 : 3 = 340 000 (đồng)
b) Nếu nhóm đó có 4 người thì trung bình mỗi người làm được:
1020 000 : 4 = 255 000 (đồng)

Tham khảo:
Gọi x, y lần lượt là số hũ tương cà loại A, loại B mà chủ nông trại cần làm.
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Có 180 kg cà chua nên \(10x + 5y \le 180\)
- Có 15 kg hành tây nên \(x + 0,25y \le 15\)
- Số hũ tương loại A ít nhất gấp 3,5 lần số hũ tương loại B nên \(x \ge 3,5y\)
Từ đó ta có hệ bất phương trình:
\(\left\{ \begin{array}{l}10x + 5y \le 180\\x + 0,25y \le 15\\x \ge 3,5y\\x \ge 0\\y \ge 0\end{array} \right.\)
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên hệ trục tọa độ Oxy.

Miền không gạch chéo (miền tam giác OAB, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
Với các đỉnh \(O(0;0),A(14;4),\)\(B(15;0).\)
Gọi F là số tiền lãi (đơn vị: nghìn đồng) thu được, ta có: \(F = 200x + 150y\)
Tính giá trị của F tại các đỉnh của tứ giác:
Tại \(O(0;0),\)\(F = 200.0 + 150.0 = 0\)
Tại \(A(14;4),\)\(F = 200.14 + 150.4 = 3400\)
Tại \(B(15;0),\)\(F = 200.15 + 150.0 = 3000\)
F đạt giá trị lớn nhất bằng \(3400\) nghìn đồng tại \(A(14;4).\)
Vậy chủ nông trại đó nên làm 14 hũ loại A và 4 hũ loại B để tiền lãi thu được là lớn nhất.

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II được nhà máy lập kế hoạch sản xuất. Khi đó số lãi nhà máy nhân được là P = 3x + 5y (nghìn đồng).
Các đại lượng x, y phải thỏa mãn các điều kiện sau:
(I)
(II)
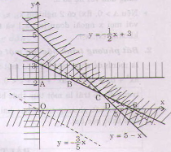
Miền nghiệm của hệ bất phương trình (II) là đa giác OABCD (kể cả biên).
Biểu thức F = 3x + 5y đạt giá trị lớn nhất khi (x; y) là tọa độ đỉnh C.
(Từ 3x + 5y = 0 => y = Các đường thẳng qua các đỉnh của OABCD và song song với đường y =
cát Oy tại điểm có tung độ lớn nhất là đường thẳng qua đỉnh C).
Phương trình hoành độ điểm C: 5 - x = <=> x = 4.
Suy ra tung độ điểm C là yc = 5 - 4 = 1. Tọa độ C(4; 1). Vậy trong các điều kiện cho phép của nhà máy, nếu sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm đơn vị loại II thì tổng số tiền lãi lớn nhất bằng:
Fc = 3.4 + 5.1 = 17 nghìn đồng.

Tham khảo:
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Tổng số giờ vẽ không quá 30 giờ nên \(2x + 3y \le 30\)
- Số tấm thiệp tối thiểu là 12 tấm nên \(x + y \ge 12\)
Từ đó ta có hệ bất phương trình: \(\left\{ \begin{array}{l}2x + 3y \le 30\\x + y \ge 12\\x \ge 0\\y \ge 0\end{array} \right.(x,y \in \mathbb{N})\)
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy, ta được như hình dưới.
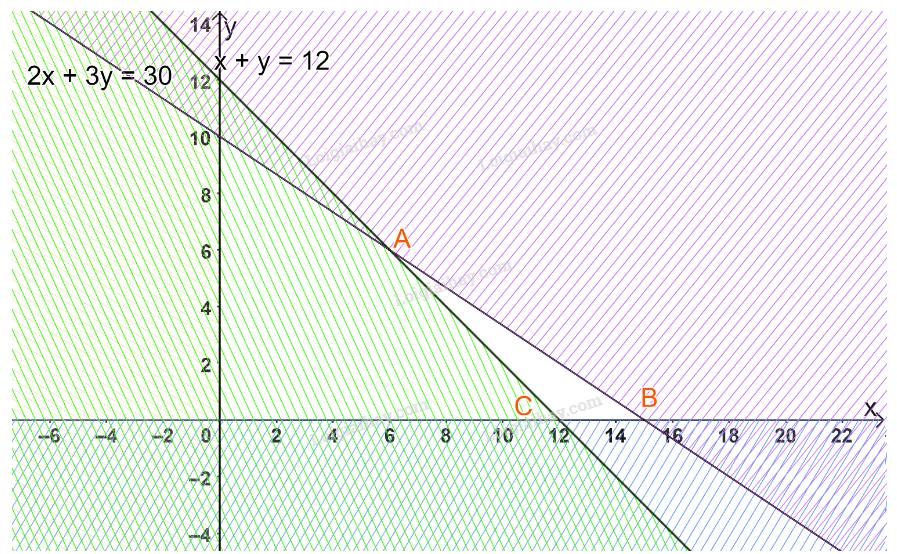
Miền không gạch chéo (miền tam giác ABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình.
Với các đỉnh \(A(6;6),\)\(B(15;0),\)\(C(12;0).\)
Gọi F là số tiền (đơn vị: nghìn đồng) thu được, ta có: \(F = 10x + 20y\)
Tính giá trị của F tại các đỉnh của tam giác:
Tại \(A(6;6):\)\(F = 10.6 + 20.6 = 180\)
Tại \(B(15;0):\)\(F = 10.15 + 20.0 = 150\)
Tại \(C(12;0):\)\(F = 10.12 + 20.0 = 120\)
F đạt giá trị lớn nhất bằng 180 tại \(A(6;6).\)
Vậy bạn học sinh đó cần vẽ 6 tấm thiệp loại nhỏ và 6 tấm thiệp loại to để có được nhiều tiền nhất.
