Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Gọi A là số tiền gửi ban đầu, n là số năm gửi.
Theo bài ra: Sau 1 năm, số tiền cả vốn lẫn lãi là : A + A. 8,4% =A. 1,084.
Sau 2 năm, số tiền cả vốn lẫn lãi là: A.1,084 + A. 1,084.8,4% = A. 1,084^2.
Sau n năm, số tiền cả vốn lẫn lãi là A. 1,084^n.
Số tiền này bằng 2 lần ban đầu nên: A. 1,084^n = 3A
ð n = ~ 14

Đáp án B
Gọi A là số tiền ban đầu người đó gửi.
Sau năm đầu, người đó nhận được số tiền là: A + A .9 % = A 1 + 9 % .
Sau năm thứ hai, người đó nhận được số tiền là: A 1 + 9 % 2 .
…
Sau năm thứ n, người đó nhận được A 1 + 9 % n .
Yêu cầu bài toán tương đương với
A 1 + 9 % n = 3 A ⇔ n = log 1 + 9 % 3 ≈ 12,7 năm.

Số tiền gửi ban đầu là A thì số tiền người đó thu về (cả gốc và lãi) sau n năm là A ( 1 + 0 , 061 ) n và số tiền lãi người đó thu về là A ( 1 + 0 , 061 ) n - A
Ta cần tìm n nhỏ nhất sao cho
A ( 1 + 0 , 061 ) n - A ≥ A ⇔ 1 , 061 n ≥ 2 ⇔ n ≥ log 1 , 061 2 ≈ 11 , 7062
Vậy sau ít nhất 12 năm người này sẽ thu về số tiền lãi ít nhất bằng số tiền ban đầu.
Chọn đáp án A.

Đáp án B
Gọi số tiền ban đầu là T. Sau n năm, số tiền thu được là:
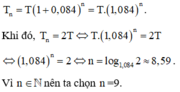

Đáp án A
Gọi số tiền ban đầu là a thì ta có ![]()
Suy ra sau 9 năm thì người đó sẽ có số tiền gấp đôi số tiền ban đầu

Đáp án C
Phương pháp:Sử dụng công thức lãi kép ![]() , trong đó:
, trong đó:
A n : tiền gốc lẫn lãi sau n năm
A: tiền vốn ban đầu.
r: lãi suất
n: năm.
Cách giải: Giả sử sau n năm người đó nhận được số tiền lớn hơn 150% số tiền gửi ban đầu.
Gọi số tiền gửi ban đầu là A ta có:
![]()
![]()
![]()
Vậy sau ít nhất 9 năm người đó nhận được số tiền lớn hơn 150% số tiền gửi ban đầu