Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi d1 là khoảng cách từ thúng gạo đến vai, với lực
P 1 = m 1 g = 30.10 = 300 ( N )
d2 là khoảng cách từ thúng ngô đến vai d 2 = 1 , 5 − d 1 , với lực
P 2 = m 2 g = 20.10 = 200 ( N )
Áp dụng công thức: P1.d1 = P2.d2 300d1 = ( 1,5 – d1).200
=>d1 = 0,6 (m ) => d2 = 0,9 ( m )
Vì hai lực song song cùng chiều, nên lực tác dụng vào vai là
F = P 1 + P 2 = 300 + 200 = 500 ( N )

Ta có: \(\dfrac{F_1}{F_2}=\dfrac{d_2}{d_1}\Leftrightarrow\dfrac{P_1}{P_2}=\dfrac{d_2}{d_1}\Leftrightarrow\dfrac{m_1.g}{m_2.g}=\dfrac{d_2}{d_1}\Leftrightarrow\dfrac{d_2}{d_1}=\dfrac{m_1}{m_2}\Leftrightarrow\dfrac{d_2}{d_1}=\dfrac{3}{6}\)
Mặt khác, ta có: \(d_1+d_2=1,2\)
\(\Rightarrow d_1=0,4m;d_2=0,8m\)

Ta có:
\(\begin{array}{l}\frac{{{F_1}}}{{{F_2}}} = \frac{{{d_2}}}{{{d_1}}} \Leftrightarrow \frac{{{P_1}}}{{{P_2}}} = \frac{{{d_2}}}{{{d_1}}} \Leftrightarrow \frac{{{m_1}.g}}{{{m_2}.g}} = \frac{{{d_2}}}{{{d_1}}}\\ \Leftrightarrow \frac{{{d_2}}}{{{d_1}}} = \frac{{{m_1}}}{{{m_2}}} \Leftrightarrow \frac{{{d_2}}}{{{d_1}}} = \frac{7}{5}\end{array}\)
Mặt khác, ta có: \({d_1} + {d_2} = 1,5\)
=> d1 = 0,625 m; d2 = 0,875 m.

Gọi d1 là cánh tay đòn của trọng lực của gạo P1→
d2 là cánh tay đòn của trọng lực của ngô P2→
Áp dụng quy tắc hợp lực hai lực song song cùng chiều:
Mặt khác: d1 + d2 = O1O2 = 1,5m (2)
Giải hệ (1), (2) ta được: d1 = 60 cm; d2 = 90cm.
Vậy vai người gánh chịu một lực là P = P1 + P2 = 300 + 200 = 500 (N), điểm đặt của vai cách đầu treo thúng gạo d1 = 60 cm.


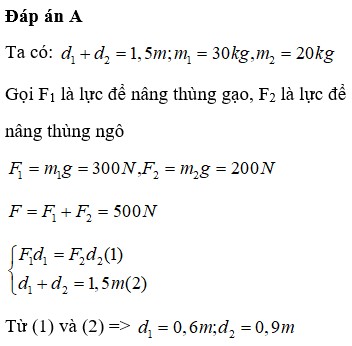


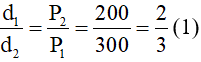
Trọng lượng của 2 vật lần lượt là:
\(P_1=10m_1=300\) (N)
\(P_2=10m_2=500\) (N)
Gọi khoảng cách từ vị trí treo đòn gánh tới vật \(m_1\) và \(m_2\) lần lượt là \(d_1\) và \(d_2\).
Để đòn gánh cân bằng thì:
\(P_1d_1=P_2d_2\)
\(\Rightarrow3d_1=5d_2\)
Mặt khác:
\(d_1+d_2=1\) (m)
\(\Rightarrow\left\{{}\begin{matrix}d_1=0,625\\d_2=0,375\end{matrix}\right.\) (m)
Vậy đòn gánh đặt vào vai cách đầu treo vật 1 là 62,5 cm.