Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Thời gian từ lúc hòn đá rơi đến lúc chạm mặt nước là:
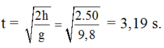

a)Phương trình quỹ đạo: \(y=\dfrac{g}{2v_0^2}x^2=\dfrac{9,8}{2\cdot5^2}x^2=0,196x^2\)
b)Thời gian hòn đá chạm mặt nước biển: \(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot10}{9,8}}=2,04s\)
c)Tầm xa vật: \(L=x_{max}=v_0t\)
Tọa độ Ox: \(\left\{{}\begin{matrix}v_{0x}=v_0\\a_x=0\\v_x=v_0\end{matrix}\right.\)
Tọa độ Oy: \(\left\{{}\begin{matrix}v_{0y}=0\\a_y=g\\v_y=gt\end{matrix}\right.\)
Độ lớn vận tốc: \(v=\sqrt{\left(gt\right)^2+v_0^2}\)
c)Sau 1s:
Tầm xa: \(L=v_0t=5\cdot1=5m\)
Độ lớn: \(v=\sqrt{\left(gt\right)^2+v_0^2}=\sqrt{\left(9,8\cdot1\right)^2+5^2}=11m/s\)

a)Thời gian hòn đá rơi chạm mặt nước biển:
\(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot10}{9,8}}=\dfrac{10}{7}s\approx1,43s\)
b)Tầm xa của vật: \(L=v_0\sqrt{\dfrac{2h}{g}}=5\cdot\sqrt{\dfrac{2\cdot10}{9,8}}=\dfrac{50}{7}m\)
Vận tốc vật khi chạm mặt nước biển:
\(v=v_0+gt=5+9,8\cdot\dfrac{10}{7}=19m/s\)

* Tóm tắt : | Giải :
\(v_0=12\) m/s | a, Thời gian hòn đá chạm mặt biển :
\(h=19,6m\) | \(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2.19,6}{9,8}}=2\left(s\right)\)
\(g=9,8\) (m/s2) | b, Tầm Xa của hòn đá :
( đề ko cho, tức | \(L=v_o.t=12.2=24\left(m\right)\)
là g = 9,8)
----------
a, \(t=?\left(s\right)\)
b, \(L=?\left(m\right)\)\(\)

Ta có: v0 = 5 m/s, h = 10 m.
a) Phương trình chuyển động của hòn đá là:
+ Ox: x = v0 .t = 5.t
+ Oy: \(y = \frac{1}{2}g{t^2} = \frac{1}{2}.9,81.{t^2} = 4,905{t^2}\)
b) Tọa độ của hòn đá sau 1 s là:
x = 5.t = 5.1 = 5 (m)
\(y = 4,905{t^2} = 4,{905.1^2} = 4,905(m)\)
c) Thời gian rơi của vật: \(t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.10}}{{9,81}}} \approx 2(s)\)
Vị trí của hòn đá ngay trước khi hòn đá chạm mặt nước biển:
\(y = 4,905.{t^2} = 4,{905.2^2} = 19,62(m)\)
Tốc độ của hòn đá trước khi chạm mặt nước biển là:
\(v = \sqrt {2gh} = \sqrt {2.9,81.10} \approx 14(m/s)\)

Đáp án A
Thời gian từ lúc hòn đá rơi đến lúc chạm mặt nước là t = 2 h g = 2.50 9 , 8 = 3 , 19