Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Ta có vận tốc trung bình v = s 1 + s 2 + s 3 t 1 + t 2 + t 3
Giai đoạn một: S 1 = S 2 mà t 1 = S 1 v 1 = S 2 v 1 = 2 120 ( h )
Giai đoạn 2: S 2 = v 2 . t 2 = 40. t 2
Giai đoạn 3: S 3 = v 3 . t 3 = 20. t 3 mà t 2 = t 3 ⇒ s 3 = 20 t 2
Theo bài ra S 2 + S 3 = S 2 ⇒ 40 t 2 + 20 t 2 = S 2 ⇒ t 2 = t 3 = S 120 ( h )
⇒ v = S S 120 + S 120 + S 120 = 40 k m / h

1)
Gọi s là quãng đường AB
Thời gian vật chuyển động trên nửa đoạn đường đầu :
t = (s/2) / v = s/(2.60) + s/120 (h)
Trên đoạn đường còn lại:
- Gọi t' là thời gian đi được.
- Quãng đường vật đi được trong nửa thời gian đầu:
s1 = v1.(t' / 2) = 40t' / 2 = 20t' (km)
- Quãng đường vật đi được trong nửa thời gian còn lại:
S2 = v2. (t'/2) = 30t' / 2 = 15t' (km)
- Vận tốc trung bình:
v' = (s1 + s2) / t' = (20t' + 15t') / t' = 35 (km/h)
Thời gian vật chuyển động trên nửa đoạn đường còn lại :
t' = (s/2) / v' = s/(2.35) = s/70 (h)
Vận tốc trung bình trên cả quãng đường :
Vtb = s / (t + t') = s / (s/120 + s/70) = 1 / (17120 + 1/70) ~ 44,2 (km/h)
Vậy...

vận tốc trung bình của người đó trên cả quãng đường là:
\(v_{tb}=\dfrac{\dfrac{t}{2}\left(v_1+v_{tb2}\right)}{t}\Rightarrow30=\dfrac{1}{2}\left(40+v_{tb2}\right)\Rightarrow v_{tb2}=20\left(\dfrac{km}{h}\right)\)
vận tốc trung bình của người đó trên phần đường còn lại là:
\(v_{tb2}=\dfrac{s_2}{\dfrac{s_2}{2}\left(\dfrac{1}{v_2}+\dfrac{1}{v_3}\right)}\Rightarrow20=\dfrac{1}{\dfrac{1}{2}\left(\dfrac{1}{30}+\dfrac{1}{v_3}\right)}\Rightarrow v_3=15\left(\dfrac{km}{h}\right)\)
vậy ...

xin lỗi hình như đề bạn còn thiếu vận tốc nửa quãng đường sau của phần đường còn lại
Bạn giải bài này theo hướng
Vận tốc trung bình của người đó trên cả quãng đường
\(v_{tb}=\dfrac{\dfrac{t}{2}\left(v_1+v_2\right)}{t}\Rightarrow\dfrac{1}{2}\left(40+v_2\right)=30\Rightarrow v_2=20\left(\dfrac{km}{h}\right)\)
vận tốc của người đó trên phần đường còn lại là
\(v_2=\dfrac{s}{\dfrac{s}{2}\left(v_3+?\right)}\Rightarrow20=\dfrac{1}{\dfrac{1}{2}\left(v_3+?\right)}\)

Gọi độ dài đoạn Ab là x(km).Gọi các đoạn(đi với vận tõc khác nhau) lần lượt là I,II,III.
Thời gian đi được trong đoạn I:
t1=s1/v1=(1/2x)/60=x/120h
Thời gian đi đoạn II:
t2=s2/v2=(1/4x)/40=x/160h
Thời gian đi đoạn III:
t3=s3/v3=(1/4x)/20=x/80h
Vận tốc trung bình trên cả đoạn đường AB(km/h)
V=(s1+s2+s3)/(t1+t2+t3)
=x/(x/120+x/160+x/80)
=x/[x/40.(1/3+1/4+1/2)]
=x/(13x/480)=480/13
=37km/h
gọi thời gian, vận tốc, nửa đoạn đường đầu lần lượt là t1, v1 , S1
gọi nửa đoạn đường sau là S2
gọi nửa thời gian đầuvà sau của nửa đoạn đường còn lại là t2 và t3
gọi vận tốc của nửa đoạn đường sau trong hai giai đoạn là v2 và v3
ta có :
vtb = \(\frac{S1+S2}{t1+t2+t3}\) =\(\frac{S}{t1+t2+t3}\) =\(\frac{S}{\frac{S1}{v1}+\frac{S2}{v2+v3}}\) =\(\frac{S}{\frac{S}{\frac{2}{v1}}+\frac{S}{\frac{2}{v2+v3}}}\) =\(\frac{S}{\frac{S}{2v1}+\frac{S}{2.\left(v2+v3\right)}}\) = \(\frac{S}{S.\left(\frac{1}{2.60}+\frac{1}{2.\left(40+20\right)}\right)}\) =\(\frac{1}{\frac{1}{120}+\frac{1}{120}}\) =\(\frac{1}{\frac{2}{120}}\) = 60 km/h

gọi t3 và t4 là hai quãng thời gian ở đoạn đường sau, t2 là tổng thời gian đi ở quãng đường sau, ta có t3=t4=1/2 của t2.
Ta có v1= 30km/h
v3=40km/h
v4=45km/h
Tính v2 = S2/t2 = S3+S4/2t3 = t3.v3+t3.v4/2t3 = t3.(v3+v4)/2t3 = v3+v4/2 = 42.5(km/h) ( 2t3 ở đây tức là 2 lần t3, thực chất là t3+t4 nhưng vì chúng bằng nhau nên để 2t3 dễ rút gọn)
Vậy vtb=S1+S2/t1+t2 = v1.t1+v2.t2/t1+t2 = 35.17(km/h)~ chỗ nào bạn xử lí rút gọn xíu nhé, nó sẽ ra là 2 trên 1 phần v1 cộng 1 phần v2 nhé, còn số liệu bài này bạn nên coi lại, vì thường thì v3 và v4 cộg lại sẽ ra số chẵn nhé.
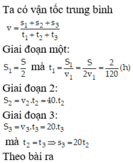
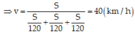

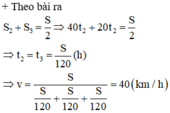


Tóm tắt
\(S_1=S_2=\dfrac{S}{2}\)
\(v_1=40km\)/h
\(v_2=60km\) /h
\(t=2h\)
\(v_{tb}=?\)
\(S=?\)
Bài làm
a) Thời gian người đó đi trên nữa quãng đường đầu là:
\(t_1=\dfrac{S_1}{v_1}=\dfrac{S}{2v_1}=\dfrac{S}{80}\left(km\right)\)
Thời gian người đó đi trên nữa quãng đường sau là:
\(t_2=\dfrac{S_2}{v_2}=\dfrac{S}{2v_2}=\dfrac{S}{120}\left(km\right)\)
Vận tốc trung bình của xe máy trên đoạn AB là:
\(v_{tb}=\dfrac{S}{t_1+t_2}=\dfrac{S}{\dfrac{S}{80}+\dfrac{S}{120}}=\dfrac{1}{\dfrac{1}{80}+\dfrac{1}{120}}=48km\)/h
Vậy vận tốc trung bình của xe máy trên đoạn AB là: 48km/h
b) Theo đề bài ta có: \(t_1+t_2=t\)
\(\Rightarrow\dfrac{S}{80}+\dfrac{S}{120}=2\)
\(\Rightarrow S=96\left(km\right)\)
Vậy quãng đường AB dài 96km
bạn có thể giải chi tiết phương trình không