Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi độ dài quãng đường AB là \(x\left(km\right)\), \(x>0\).
Thời gian người đó đi \(\frac{1}{3}\)quãng đường đầu là: \(\frac{\frac{1}{3}x}{20}=\frac{x}{60}\)(giờ)
Thời gian người đó đi quãng đường còn lại là: \(\frac{\frac{2}{3}x}{10}=\frac{x}{15}\)(giờ)
Vận tốc trung bình trên quãng đường AB của người đó là: \(\frac{x}{\frac{x}{60}+\frac{x}{15}}=\frac{1}{\frac{1}{60}+\frac{1}{15}}=12\left(km/h\right)\).


Tham khảo:
bài toán 1 :
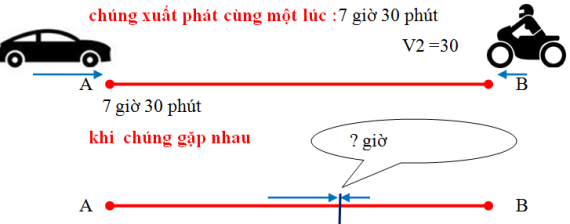
Cùng lúc 7 giờ 30 phút sáng có một ô tô đi từ tỉnh A đến tỉnh B với vận tốc 40km/h và một xe máy đi từ tỉnh B đến tỉnh A với vận tốc 30km/h. khoảng cách tỉnh A đến tỉnh B là 140 km. Hỏi hai xe gặp nhau bằng bao nhiêu mấy giờ ?
giải.
tổng hai vận tốc :
40 + 30 = 70 km/h.
thời gian gặp nhau của hai xe :
140 : 70 = 2 giờ.
hai xe gặp nhau lúc :
7 giờ 30 phút + 2 giờ = 9 giờ 30 phút.
Tham khảo nhé:
Câu hỏi của Lê Hải Anh - Toán lớp 6 - Học toán với OnlineMath

Vận tốc trung bình của người đó là:
(15 + 12 + 60) : 3 = 29 ( km/h )
AB=BC/2=3CD
AB/3=BC/6=CD/1=AD/10
vtb=AD/(tab+tbc+tcd)
tab=AB/60=AD/200
tbc=BC/48=AD/80
tcd=CD/40=AD/400
Vtb=1/(1/200+1/80+1/400)=400/(2+5+1)=400/8
vtb=50km/h