Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
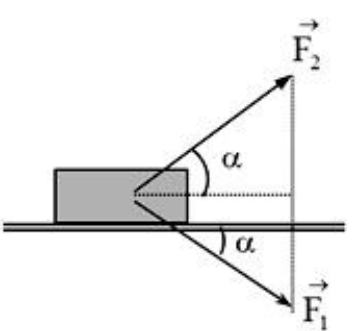
Trước hết ta tìm gia tốc a chuyển động của toa xe trên mặt phẳng nghiêng
Theo định luật II Niu-tơn :
Xét theo phương Oy vuông góc với mặt phẳng nghiêng :
Phản lực : N = mgcos α
Lực ma sát F = μ N = μ m g cos α
Xét theo phương Ox của mặt phẳng nghiêng thì :
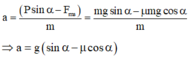
Với β = 90 0 - α ⇒ cos β = sin α , với F = ma
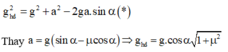
Chu kì dao động bé của con lắc đơn : T = 2 π 1 g hd = 2 π 1 gcosα 1 + μ 2
Từ những dữ kiện trên ta thay số vào tính được : v m a x = 0 , 21 m / s

Xe chuyển động trên chiếc cầu cong vòng.
Coi xe chuyển động tròn đều, lực phát động khi đó cân bằng với lực ma sát.
Xe chịu tác dụng của hai lực cân bằng khi ở điểm cao nhất của cầu là trọng lượng xe và phản lực của xe lần lượt \(\overrightarrow{P};\overrightarrow{N}\)
Ta có: \(\overrightarrow{F_{ht}}=m\cdot\overrightarrow{a_{ht}}=\overrightarrow{P}+\overrightarrow{N}\)
\(\Rightarrow F_{ht}=P-N\)
\(\Rightarrow\)Áp lực do xe gây ra nhỏ hơn trọng lượng xe.
Chọn A.

Toa xe trượt không ma sát trên đường dốc với góc nghiêng \(\alpha\)
Ta có kết quả:
+ Khi vật ở VTCB thì phương của sợi dây vuông góc với mặt phẳng nghiêng.
+ Gia tốc hiệu dụng của vật: \(g'=g.\cos\alpha\)
Chu kì dao động: \(T=2\pi\sqrt{\dfrac{\ell}{g'}}=2\pi\sqrt{\dfrac{1,5}{10.\cos 45^0}}\approx2,89(s)\)

Toa xe trượt không ma sát trên đường dốc với góc nghiêng \(\alpha\)
Ta có kết quả:
+ Khi vật ở VTCB thì phương của sợi dây vuông góc với mặt phẳng nghiêng.
+ Gia tốc hiệu dụng của vật: \(g'=g.\cos a\)
Chu kì dao động: \(T=2\pi\sqrt{\frac{l}{g'}}=2\pi\sqrt{\frac{1,5}{10.\cos45^o}}\approx2,89\left(s\right)\)

Chọn A
+ Nước trong xô sóng sánh mạnh nhất khi tần số xe đạp gặp rãnh trùng với tần số dao động riêng của nước trong thùng. Tần số f = 1/T = 1 (Hz).
=> Nước trong thùng sóng sánh mạnh nhất khi xe đi với vận tốc không có lợi v = S/T = 5/1 = 5 (m/s) = 18 (km/h)