Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Khi hòn đá ở đỉnh của đường tròn thì trọng lực và lực căng dây đóng vai trò là lực hướng tâm:
Fht = P + T
→ T = Fht - P
T = mω2r – mg
= 0,4.05 – 0,4.9,8 = 8,88 N.

Chọn A.
Khi hòn đá ở đỉnh của đường tròn thì trọng lực và lực căng dây đóng vai trò là lực hướng tâm: Fht = P + T → T = Fht - P
⟹ T = mω2r – mg = 0,4.82.0,5 – 0,4.9,8 = 8,88 N.

Đáp án A
Khi hòn đá ở đỉnh của đường tròn thì trọng lực và lực căng dây đóng vai trò là lực hướng tâm.


Chọn A.
Khi hòn đá ở đỉnh của đường tròn thì trọng lực và lực căng dây đóng vai trò là lực hướng tâm:
F h t = P + T → T = F h t - P
⟹ T = m ω 2 r – mg
= 0,4. 8 2 .0,5 – 0,4.9,8 = 8,88 N.

Khi hòn đá ở điểm thấp nhất của quỹ đạo thì trọng lượng và lực căng dây đóng vai trò là lực hướng tâm.
F h t = P + T → T = F h t − P = m ω 2 r − m g = 0 , 4.8 2 .0 , 5 − 0 , 4.10 = 8 , 8 N
Đáp án: B
Thế còn đối với trường hợp điểm C sao cho sợi dây hợp với phương thẳng đứng góc 60° thì tính như thế nào bạn, mong bạn giải đáp

a) Tốc độ dài:
\(v=r.\omega=0,5.8=4\left(m/s\right)\)
Chu kì:
\(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{8}=\dfrac{1}{4}\pi\left(s\right)\)
Tần số:
\(f=\dfrac{1}{T}=\dfrac{1}{\dfrac{1}{4}\pi}\approx1,27\left(\text{vòng/s.}\right)\)
b) Lực hướng tâm:
\(F_{ht}=\dfrac{m.v^2}{r}=\dfrac{0,4.4^2}{0,5}=12,8\left(N\right)\)
c) Khi hòn đá ở điểm thấp nhất của quỹ đạo thì trọng lượng và lực căng dây đóng vai trò là lực hướng tâm:
\(F_{ht}=P+T\Leftrightarrow T=F_{ht}-P=12,8-mg=12,8-0,4.10=8,8\left(N\right)\)

Ta có: \(F_{ht}=mg+T\)
\(\Leftrightarrow T^2=\left(mg\right)^2+F_{ht}^2\left(Pytago\right)\)
\(\Leftrightarrow T^2=F_{ht}^2+\left(mg\right)^2=\left(\dfrac{mv^2}{R}\right)+\left(mg\right)^2\)
\(\Rightarrow m=\dfrac{T}{\sqrt{g^2+\dfrac{v^4}{R^2}}}\approx0,8\left(kg\right)\)

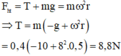
Khi hòn đá ở điểm thấp nhất của quỹ đạo thì trọng lượng và lực căng dây đóng vai trò là lực hướng tâm.
F h t ¯ = P → + T →
= > F h t = P − T = > T = P + F h t = m g + m ω 2 r
= 0,4.10 + 0,4.8 2 .0,5 = 16,8 N
Đáp án: C