Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(p=\dfrac{F}{S}=\dfrac{mg}{S}\)
Nhìn vô đây ta thấy S càng lớn thì p càng nhỏ, vậy
\(p_{min}\Leftrightarrow S_{max}=0,2.0,1=0,02\left(m^3\right)\Rightarrow p_{min}=\dfrac{10.600.0,2.0,1.0,05}{0,02}=...\left(Pa\right)\)
\(p_{max}\Leftrightarrow S_{min}=0,1.0,05=0,005\left(m^3\right)\)
\(\Rightarrow p_{min}=...\left(Pa\right)\)

Thể tích khối lim loại đó là : \(V=20.40.50=40000\left(cm^3\right)=0,04\left(m^3\right)\)
Khối lượng riêng là : \(D=\frac{d}{10}=\frac{78500}{10}=7850\left(kg/m^2\right)\)
Khối lượng của khối lim loại đó là : \(m=D.V=7850.0.04=314\left(kg\right)\)
Diện tích phần mặt phẳng tiếp xúc là : \(S=40.50=2000\left(cm^2\right)=0,2\left(m^2\right)\)
Áp lực của khối kim loại tác dụng lên mặt phẳng ngang là : \(F=10m=10.314=3140\left(N\right)\)
Áp suất do khối kim loại tác dụng lên mặt phẳng ngang là : \(P=\frac{F}{S}=\frac{3140}{0,2}=15700\left(Pa\right)\)

Đáp án C
- Trọng lượng của viên gạch là:
1,2.10 = 12 (N)
- Áp suất của viên gạch tác dụng lên mặt bàn nhỏ nhất khi diện tíc tiếp xúc lớn nhất.
- Diện tích tiếp xúc lớn nhất là: 20.10 = 200 ( c m 2 ) = 0,02 ( m 2 )
20.10 = 200 ( c m 2 ) = 0,02 ( m 2 )
- Áp suất nhỏ nhất mà viên gạch tác dụng vào mặt bàn là:
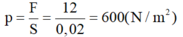

\(20cm=0,2m;10cm=0,1m;5cm=0,05m\)
\(\left\{{}\begin{matrix}p'=dh'=2\cdot10^4\cdot0,2=4000\left(Pa\right)\\p''=dh''=2\cdot10^4\cdot0,1=2000\left(Pa\right)\\p'''=dh'''=2\cdot10^4\cdot0,05=1000\left(Pa\right)\end{matrix}\right.\)
\(\Rightarrow p'>p''>p'''\)
\(\Rightarrow\left\{{}\begin{matrix}p_{max}=4000\left(Pa\right)\\p_{min}=1000\left(Pa\right)\end{matrix}\right.\)
Chọn A

\(V=20.10.5=1000cm^3=10^{-3}m^3\)
\(P=dV=18400.10^{-3}=18,4\left(N\right)\)
\(D=\frac{1}{10}d\Rightarrow18400:10=1840\left(\frac{kg}{m^3}\right)\)
\(F=P=18,4N\)
Diện tích bị ép nhỏ nhất là: \(S_1=20.10=200cm^2=2.10^{-2}cm^2\)
Áp suất nhỏ nhất là: \(p_1=\frac{F_1}{S_1}=\frac{18,4}{2.10^{-2}}=920\left(Pa\right)\)
Diện tích bị ép lớn nhất là: \(S_1=10.5=50cm^2=5.10^{-3}cm^2\)
Áp suất lớn nhất là \(p_2=\frac{F}{S_2}=3680\left(Pa\right)\)