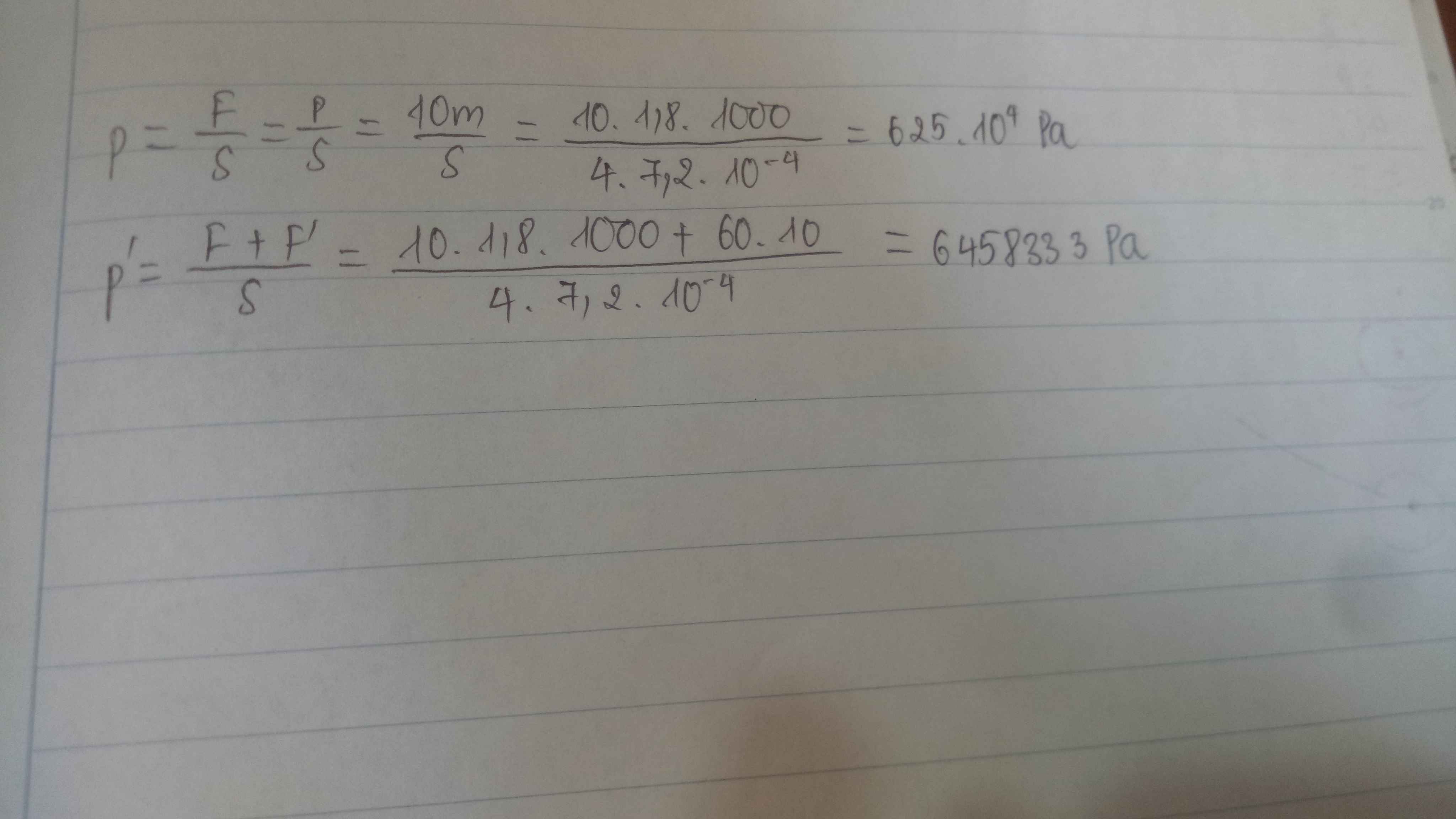Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tóm tắt:
\(F_1=400 000N\)
\(S_1=200dm^2=2 m^2\)
\(F_2=2000kg=20000N\)
\(S_2=0,025m^2\)
___________________
\(a, P_1=?\)
\(P_2=?\)
b, Xe nào dễ sa lầy?Vì sao?
Giải:
a,Áp suất của máy kéo lên mặt đường là:
\(P_1=\dfrac{F_1}{S_1}=\dfrac{400000}{2}=200000(Pa)\)
Áp suất của ô tô lên mặt đường là:
\(P_2=\dfrac{F_2}{S_2}=\dfrac{20000}{0,025}=800000(Pa)\)
b) Nhận xét: \(P_1 < P_2 (200000<800000) \) .Vậy nếu đi trên đất mềm, ô tô dễ bị sa lầy hơn.

Áp suất của xe tăng lên mặt đường nằm ngang là:
Pxe = =
= 226 666,6 N/m2
Áp suất của ôtô lên mặt đường nằm ngang là:
Pôtô = =
= 80 N/cm2 = 800 000 N/m2
Áp suất của xe tăng lên mặt đường nằm ngang còn nhỏ hơn nhiều lần áp suất của ôtô. Do đó xe tăng chạy đc trên đất mềm.
Máy kéo nặng nề hơn ôtô lại chạy được trên đất mềm là do máy kéo dùng cích có bản rộng nên áp suất gây ra bởi trọng lượng của máy kéo nhỏ. Còn ôtô dùng bánh (diện tích bị ép nhỏ), nên áp suất gây ra bởi trọng lượng của ôtô lớn hơn.
Đổi 250 cm2 = 0,025m2
Áp xuất của xe tăng lên mặt đường :
p=\(\dfrac{F}{S}\) = \(\dfrac{340000}{1,5}\) \(\approx\)226666 N/m2
Áp xuất của ô tô lên mặt đường :
p=\(\dfrac{F}{S}\)=\(\dfrac{20000}{0.025}\)= 800000 N/m2

Đổi S2 = 250 cm2 = 0,025 m2
Áp suất của xe tăng lên mặt đường là:
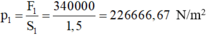
Áp suất của xe ô tô lên mặt đường là:
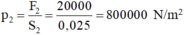
Như vậy, áp suất của xe ô tô lên mặt đường lớn hơn áp suất của xe tăng lên mặt đường.
Sở dĩ máy kéo chạy được bình thường trên nền đất mềm còn ô tô thì rất khó chạy trên nền đất mềm và thường bị sa lầy vì máy kéo có các bản xích giống như xe tăng, áp suất do máy kéo tác dụng xuống mặt đường nhỏ hơn so với áp suất của ô tô tác dụng xuống mặt đường.

\(\left\{{}\begin{matrix}p_1=\dfrac{F_1}{S_1}=\dfrac{P_1}{S_1}=\dfrac{360000}{1,5}=240000\left(Pa\right)\\p_2=\dfrac{F_2}{S_2}=\dfrac{P_2}{S_2}=\dfrac{15000}{250}=60\left(Pa\right)\end{matrix}\right.\)

2000 kg = 20000 N
Áp suất của ô tô tác dụng lên mặt đường là
\(p=\dfrac{F}{S}=20000:0,025=800000\left(Pa\right)\)

Áp suất của ô tô là
p=\(\dfrac{F}{S}\)=\(\dfrac{20000}{0,025}\)=800000(Pa)