Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức tính năng lượng điện từ trường ta có
W = Wđ = Wt \(\Rightarrow\frac{1}{2}LI_0^2=\frac{1}{2}lI^2+\frac{1}{2}Cu^2\)
\(\Rightarrow u=\sqrt{\left(I_0^2-I^2\right)\frac{L}{C}}\Rightarrow u=\)\(\sqrt{\frac{0,1}{10^{-5}}\left(0,05^2-0,02^2\right)}=4\left(V\right)\)
chọn A

Đáp án B
Phương pháp: Áp dụng bảo toàn năng lượng trong mạch LC
Cách giải:
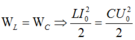
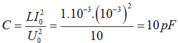

Hiệu điện thế cực đại giữa hai bản tụ trong khung dao động bằng 6V6V, điện dung của tụ bằng 1μF1μF . Biết dao động điện từ trong khung năng lượng được bảo toàn, năng lượng từ trường cực đại tập trung ở cuộn cảm bằng
A.18.10-6 J.
B.0,9.10-6 J.
C.9.10-6 J.
D.1,8.10-6 J.

Điện dung của tụ điện: \(C=\dfrac{\varepsilon S}{4\pi k d}\), nên C tỉ lệ thuận với hằng số điện môi \(\varepsilon\) và tiết diện \(S\)
Gọi C là điện dung của tụ khi không có điện môi, suy ra khi có điện môi thì điện dung là \(C_1=\varepsilon C\)
Khi rút tấm điện môi ra sao cho tấm điện môi chỉ chiếm một nửa không gian tụ, lúc này ta coi tụ gồm hai bản tụ nối song song, trong đó 1 tụ không có điện môi, một tụ chứa đầy điện môi. Điện dung của tụ lúc này là: \(C_2=\dfrac{C}{2}+\dfrac{\varepsilon C}{2}=\dfrac{1+\varepsilon}{2}.C\)
Khi dòng điện tức thời của mạch cực đại thì năng lượng của tụ bằng 0, do vậy thao tác trên tụ thì năng lượng của mạch LC vẫn bảo toàn.
\(W_1=W_2\Rightarrow C_1.U_{01}^2=C_2.U_{02}^2\)
\(\Rightarrow U_{02}=U_{01}\sqrt{\dfrac{C_1}{C_2}}=U_{01}.\sqrt{\dfrac{2\varepsilon}{1+\varepsilon}}=6\sqrt 3.\sqrt {\dfrac{4}{3}}=12(V)\)
Chọn B.

Ta có: \(W=W_t+W_d\)
\(\Leftrightarrow W_t=W_{dmax}-W_d\)
\(=\frac{1}{2}C.U^2_0-\frac{1}{2}Cu^2\)
\(=5.10^{-5}J\)

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

\(T = 2\pi .\sqrt{LC} = 2.10^{-5}s.\)
Thời gian từ lúc hiệu điện thế trên tụ cực đại U0 đến lúc hiệu điện thế trên tụ \(+\frac{U_0}{2}\) tính dựa vào đường tròn
U 0 +U 0 2
\(\cos \varphi = \frac{U_)/2}{U_0}= \frac{1}{2}=> \varphi= \frac{\pi}{3}. \)
\( t = \frac{\varphi}{\omega}= \frac{\pi/3}{2\pi/T}= \frac{T}{6}= \frac{1}{3}.10^{-5}s.\)
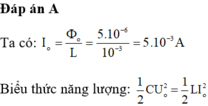
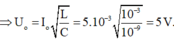

Đáp án A
Phương pháp: Áp dụng công thức tính suất điện động cực đại
Cách giải:
Theo bài ra ta có: