Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn: Chọn đáp án D
Khoảng thời gian ngắn nhất kể từ lúc năng lượng từ trường đạt giá trị cực đại (giả sử lúc này i = I 0 ) đến khi năng lượng trên tụ bằng ba lần năng lượng trên cuộn cảm (lúc này i = I 0 2 ) là
T 6 = π 6 10 − 6 ⇒ T = π .10 − 6 ( s ) ⇒ ω = 2 π T = 2.10 6 (rad/s)
Trường hợp này nạp năng lượng cho cuộn cảm nên I 0 = E r , do đó, từ công thức tính năng lượng dao động:
W = Q 0 2 2 C = L I 0 2 2 = L 2 E r 2
⇒ E = Q 0 ω r = 2.10 − 6 .2.10 6 .2 = 8 ( V )

chọn đáp án B
Khoảng thời gian ngắn nhất từ lúc năng lượng điện trường cực đại đến lúc năng lượng từ trường cực đại là
T 4 = 5.10 − 9 ⇒ T = 2.10 − 8 ⇒ ω = 2 π T = 10 8 π (rad/s)
⇒ L = 1 ω 2 C = 0,001 ( H )
Đây là trường hợp nạp năng lượng cho cuộn cảm nên I 0 = E r , do đó, từ công thức tính năng lượng dao động
W = L I 0 2 2 = L 2 E r 2
⇒ 4,5.10 − 3 = 0,001 2 E 1 2 ⇒ E = 3 ( V )

Hướng dẫn: Chọn đáp án B
Khoảng thời gian ngắn nhất từ lúc năng lượng điện trường cực đại đến lúc năng lượng từ trường cực đại là
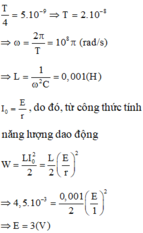

\(W= W_{Cmax}=W_C+W_L\)
=> \(W_L = W_{Cmax}-W_C= \frac{1}{2}C.(U_0^2-u^2)= 5.10^{-7}J.\)





Chọn đáp án D
Khoảng thời gian ngắn nhất kể từ lúc năng lượng từ trường đạt giá trị cực đại (giả sử lúc này i = I 0 ) đến khi năng lượng trên tụ bằng ba lần năng lượng trên cuộn cảm (lúc này i = I 0 2 ) là
T 6 = π 6 10 − 6 ⇒ T = π .10 − 6 ( s ) ⇒ ω = 2 π T = 2.10 6 (rad/s)
Trường hợp này nạp năng lượng cho cuộn cảm nên I 0 = E r , do đó, từ công thức tính năng lượng dao động:
W = Q 0 2 2 C = L I 0 2 2 = L 2 E r 2
⇒ E = Q 0 ω r = 2.10 − 6 . 2.10 6 . 2 = 8 ( V )