Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Phương pháp: Áp dụng công thức tính chu kỳ của mạch dao động LC : T = 2 π LC
Áp dụng công thức tính chu kỳ của mạch dao động ta có
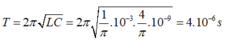
Đáp án D
Ban đầu tần số dao động riêng là: f = 2 π c L C
Sau đó mắc nối tiếp với tụ điện có điện dung C/3 thì điện dung tổng lúc này sẽ là: C = C . C 3 C + C 3 = C 4
Vậy tần số dao động riêng lúc này là: f 2 = 2 π c L C 2 = 2 π c L C 4 = 1 2 f
Đáp án D
Ta có:
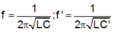
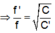
Vì C’ gồm C và C 3 mắc nối tiếp nhau nên:
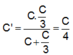
Từ đó:
Đáp án C
Ban đầu tần số dao động riêng là:
Sau đó mắc nối tiếp với tụ điện có điện dung C/3 thì điện dung tổng lúc này sẽ là:
Vậy tần số dao động riêng lúc này là:
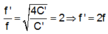
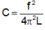
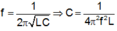
Đáp án D
Tần số dao động điện từ riêng của mạch được tính theo công thức f = 1 2 π LC .