Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số HS chỉ khá tự nhiên:
25-10=15(học sinh)
Số HS chỉ khá xã hội:
24 -10=14(học sinh)
Số HS chỉ khá 1 nhóm môn:
15+14=29(học sinh)
Đ.số: 29 học sinh

Sơ đồ học sinh lớp 10A: 25 bạn 20 bạn 15 bạn 5 1 6 7
Số học sinh thích môn toán và tiếng anh và văn là:(25+15+20)-(5+7+1+6)=42(bạn)
Số học sinh không thích môn nào là:45-42=3(học sinh)
eh8 ihgggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggg

Gọi A,B,C là tập hợp các học sinh tích môn toán , Văn , Anh
ta có :
\(\hept{\begin{cases}\left|A\right|=10,\left|B\right|=20,\left|C\right|=25\\\left|A\cap B\cap C\right|=3\\\left|A\cup B\cup C\right|=40\end{cases}}\) ta có : \(\left|A\cup B\cup C\right|=\left|A\right|+\left|B\right|+\left|C\right|-\left(\left|A\cap B\right|+\left|B\cap C\right|+\left|C\cap A\right|\right)+\left|A\cap B\cap C\right|\)
nên \(\left|A\cap B\right|+\left|B\cap C\right|+\left|C\cap A\right|=18\)
Do đó số học sinh chỉ thích đúng hai môn là :
\(\left|A\cap B\right|+\left|B\cap C\right|+\left|C\cap A\right|-3\left|A\cap B\cap C\right|=18-3\times3=9\)

Gọi x, y, z lần lượt là số học sinh đạt loại giỏi một môn, hai môn và ba môn. Lập sơ đồ Ven liên hệ giữa các tập hợp, ta có hệ phương trình:
x + y + z = 45 − 7 x + 2 y + 3 z = 20 + 18 + 17 z = 5 ⇔ x = 26 y = 7 z = 5.
Vậy số học sinh đạt loại giỏi một môn là 26 em.
Đáp án B

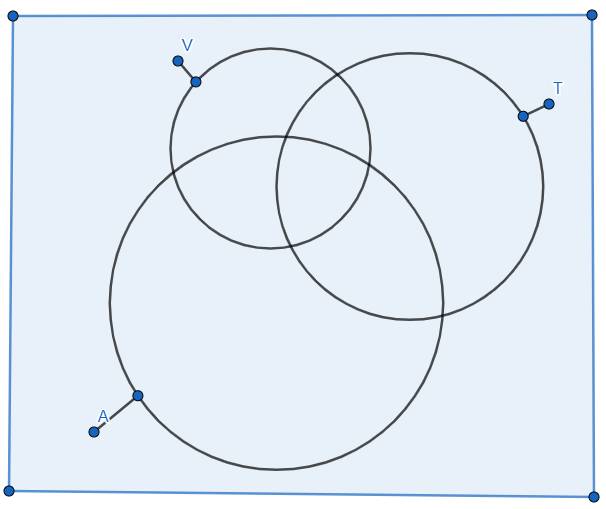
Gọi V, T, A lần lượt là tập hợp các học sinh giỏi Văn, Toán, Tiếng Anh. Theo đề bài, ta có: \(\left|V\right|=18;\left|T\right|=20;\left|A\right|=22\)\(;\left|V\cap T\cap A\right|=5\)\(;\left|A\cup T\cup V\right|=34\)
Áp dụng công thức bù trừ, ta có:
\(\left|V\cup T\cup A\right|=\left|V\right|+\left|T\right|+\left|A\right|-\left|V\cap T\right|-\left|T\cap A\right|-\left|A\cap V\right|+\left|V\cap T\cap A\right|\)
\(\Rightarrow34=18+20+22-P+5\) (với \(P=\left|V\cap T\right|+\left|T\cap A\right|+\left|A\cap V\right|\))
\(\Rightarrow P=31\)
Số học sinh thích đúng 1 môn trong 3 môn Toán, Văn, Tiếng Anh chính bằng:
\(\left|V\cup T\cup A\right|-P+2\left|V\cap T\cap A\right|\) \(=34-31+2.5=13\) (học sinh)

Số em không thích Toán là 35-25=10(bạn)
Số em không thích Văn là 35-20=15 bạn
Số em không thích Văn nhưng thích Toán là 15-8=7 bạn
SỐ em không thích Toán nhưng thích Văn là 10-8=2 bạn
SỐ em thích cả Toán và Văn là:
35-8-7-2=35-17=18 bạn

Gọi A, B lần lượt là tập hợp các học sinh thích môn Toán và Tiếng Anh, X là tập hợp học sinh lớp 10H.
Theo giả thiết, \(n(A) = 20,n(B) = 16,n(A \cap B) = 12,n(X) = 35\)

a) Nhận thấy rằng, nếu tính tổng \(n(A) + n(B)\) thì ta được số học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh, nhưng số học sinh thích cả hai môn Toán và Tiếng Anh được tính hai lần. Do đó, số học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh là:
\(n(A \cup B) = n(A) + n(B) - n(A \cap B) = 20 + 16 - 12 = 24\)
b) Trong số 35 học sinh lớp 10H, có 24 học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh, còn lại số học sinh không thích cả hai môn này là: \(35 - 24 = 11\) (học sinh).
Số học sinh chỉ học giỏi môn Toán là: 15 - [(8 - 2) + (5 - 2) + 2] = 4
Số học sinh chỉ học giỏi môn Văn là: 16 - [(5 - 2) + (6 - 2) + 2] = 7
Số học sinh chỉ học giỏi môn Tiếng Anh là: 17 - [(8 - 2) + (6 - 2) + 2] = 5
Số học sinh không học khá môn nào trong lớp học đó là: 40 - [4 + 7 + 5 + (5 - 2) + (8 - 2) + (6 - 2) + 2] = 9