Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
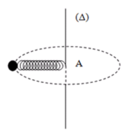
Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm.
Khi trục Δ quay thì lò xo giãn ra một đoạn Δ l
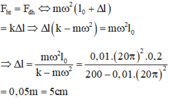

Chọn A.
Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm.
Khi trục Δ quay thì lò xo giãn ra một đoạn ∆ℓ.
Fht = Fdh ↔ mω2(ℓo + ∆ℓ) = k.∆ℓ → (k – mω2).∆ℓ = mω2ℓo


Chọn đáp án A
Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm.
Khi trục ∆ quay thì lò xo giãn ra một đoạn ∆ℓ.
Fht = Fdh
<-> mω2(ℓo + ∆ℓ) = k.∆ℓ
→ (k – mω2).∆l = mω2ℓo
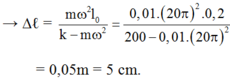

Ta có: ω = 2 π f = 2 π 360 60 = 12 π
Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm:
Khi trục Δ quay thì lò xo dãn một đoạn Δl
→ F h t = F d h ↔ m ω 2 ( l 0 + Δ l ) = k Δ l → Δ l ( k − m ω 2 ) = m ω 2 l 0 → Δ l = m ω 2 l 0 k − m ω 2 = 0 , 01. ( 12 π ) 2 0 , 4 125 − 0 , 01. ( 12 π ) 2 = 0 , 0513 m = 5 , 13 c m
Đáp án: C

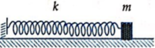
a/ \(W=\dfrac{1}{2}kx^2+\dfrac{1}{2}mv^2=\dfrac{1}{2}k\Delta l^2\)
\(\Leftrightarrow kx^2+mv^2=k\Delta l^2\Leftrightarrow v=\sqrt{\dfrac{k\Delta l^2-kx^2}{m}}=\sqrt{\dfrac{40.0,02^2-40x^2}{0,4}}\left(m/s\right)\)
b/ \(v_{max}\Leftrightarrow\dfrac{40.0,02^2-40x^2}{0,4}\left(max\right)\Leftrightarrow x=0\) => khi nó ở VTCB
\(\Rightarrow v_{max}=\dfrac{40.0,02^2}{0,4}\left(m/s\right)\)

a.Ta có ω = 2 π f = 2 π .2 = 4 π r a d / s
Khi vật quay tròn đều F d h = F q t l t ⇒ k . Δ l = m . r . ω 2
Mà r = l 0 + Δ l ⇒ k . Δ l = m . l 0 + Δ l . ω 2 ⇒ 12 , 5. Δ l = 0 , 01. 0 , 2 + Δ l . 4 π 2
⇒ Δ l = 0 , 03 m = 3 c m
b. Theo bài ra r max = l max = 0 , 4 m
⇒ F d h ≥ F q t l t ⇒ k . Δ l ≥ m . r . ω 2 ⇒ ω ≤ k . Δ l m . r
Mà Δ l = l 1 − l 0 = 40 − 20 = 20 c m = 0 , 2 m
⇒ ω ≤ 12 , 5.0 , 2 0 , 01.0 , 4 = 25 r a d / s Vậy n = 25.60 2. π = 238 , 73 ( vòng/ phút )

Đáp án C
Cơ năng của vật lúc đầu (buông nhẹ) là
![]()
![]()
Cơ năng của vật lúc sau (trạng thái có độ biến dạng ∆ l 1 = 1cm)
![]()
![]()
Do vật chịu tác dụng thêm lực ma sát ca năng của vật sẽ biến đổi. Công của các lực cản bằng độ biến thiên cơ năng của vật:
![]()



Chọn A
Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm.
Khi trục quay thì lò xo giãn ra một đoạn Δl
F h t = F d h ↔ m ω 2 ( l 0 + Δℓ) = k.Δℓ → (k – m ω 2 ).Δℓ = m ω 2 l 0