Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Góc lệch của tia sáng khi qua lăng kính trong trường hợp góc chiết quang nhỏ:
\(D = (n-1).A = (1,65-1).8 = 5,2^0\)
Chọn C

Chọn B.
Công thức tính góc lệch đối với lăng kính có góc chiết quang nhỏ và góc tới nhỏ là D = (n – 1)A = 5,20..

Đáp án A
Góc lệch của tia đỏ và tia tím qua lăng kính:
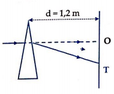

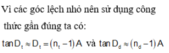
Vậy độ rộng quang phổ là:
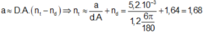

Đáp án: A
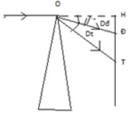
- So với phương tia tới OH, tia đỏ OĐ bị lệch một góc:
Dđ = A(n - 1) = 8.(1,5 - 1) = 4 o
- tia tím OT lệch so với phương OH một góc :
Dt = A.(n - 1) = 8.(1,54 - 1) = 4,32o
Bề rộng quang phổ trên màn là miền ĐT, ta có:
ĐT = TH - ĐH = OH.tanDt - OH.tanDđ = OH.(tan Dt - tan Dđ)
Thay số: ĐT = 1,5.(tan4,32o - tan4o ) = 8,42.10-3 m

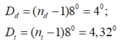
Độ rộng vùng quang phổ được tính
MN = HM – HN = AH(tanDt – tanDd) = 1,5(tan4,32o– tan4o) = 8,42.10−3 m = 8,42 mm.
Đáp án C

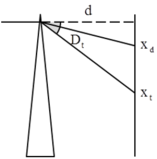
Góc giữa tia sáng đỏ và tia sáng tím sau khi ra khỏi lăng kính là
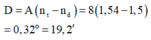
Đáp án C

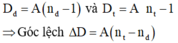
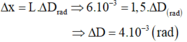
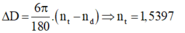
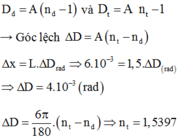
Áp dụng định luật khúc xạ
\(n_1\sin i_1 = n_2\sin r_1\)
\(n_1\sin i_2 = n_2\sin r_2\)
\(n_1;n_2\) lần lượt là chiết suất của nước và thủy tinh đối với ánh sáng đơn sắc.
Do góc \(i_1,i_2,r_1,r_2\)đều là các góc nhỏ hơn \(10^0\) => áp dụng gần đúng \(\sin i \approx i\)
=> \(n_1 (i_1+i_2) = n_2 (r_1+r_2)\)
Mà góc chiết quang \(A = r_1+r_2\)
=> \(n_1 (i_1+i_2) = n_2A\)
=> \(i_1+i_2 = A\frac{n_2}{n_1}\)
Góc lệch giữa tia tới và tia ló ra khỏi lăng kính là \(D = i_1+i_2 -A\)
=> \(D = \frac{n_2}{n_1}A-A = A(\frac{n_2}{n_1} - 1)\)
=> \(n_2 = 1,34.(\frac{2}{8}+1) = 1,675.\)
Chọn đáp án.B.1,675.