Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mặt phẳng khung dây hợp với đường cảm ứng từ một góc 300 => α= 600
\(\left|\phi\right|=\left|NBScos\alpha\right|=\left|1.5.10^{-2}.12.10^{-4}.cos60^0\right|=3.10^{-5}\)Wb

Từ thông cực đại: \(\phi_0=N.B.S = 2000.10^{-2}.0,2^2=0,8Wb\)
t = 0 chọn lúc mặt phẳng khung dây vuông góc với đường sức, có nghĩa véc tơ pháp tuyến của khung trùng với đường sức
\(\Rightarrow \varphi =0\)
Vậy biểu thức từ thông: \(\phi=0,8.\cos(100\pi t)(Wb)\)

Đáp án C
Φ t r u o c = B S cos 0 ° = 0 , 01.0 , 05.0 , 05. cos 0 ° = 2 , 5.10 − 5 W b .
Φ s a u = B S cos 90 ° = 0 , 01.0 , 05.0 , 05. cos 90 ° = 0 W b .
Δ Φ = Φ s a u − Φ t r u o c = − 2 , 5.10 − 5 W b .

Một khung dây hình vuông có cạnh dài 5 cm , đặt trong từ trường đều có cảm ứng từ B = 4.10-5 T , mặt phẳng khung dây tạo với các đường sức từ một góc 300 . Từ thông qua mặt phẳng khung dây nhận giá trị nào sau đây ?
A. 5.10-8 Wb
B. 5.10-6 Wb
C. 8.5.10-8 Wb
D. 8.5.10-6 Wb
giải thích
Mặt phẳng khung dây tạo với các đường sức từ một góc 30o nên
Khung dây hình vuông, cạnh dài 5cm có diện tích: S = 0,052 = 2,5.10-3 m2.
Từ thông qua mặt phẳng khung dây là: Φ = B.S.cosα = 4.10-5.2,5.10-3.cos60o = 5.10-8Wb

a/ \(\phi=N.BS\cos\left(\overrightarrow{B};\overrightarrow{n}\right)=200.10^{-4}.20.10^{-4}.\cos30^0=2\sqrt{3}.10^{-5}\left(T.m^2\right)\)
b/ \(E_c=\left|\frac{\Delta\phi}{\Delta t}\right|=\left|\frac{-2\sqrt{3}.10^{-5}}{0,01}\right|=2\sqrt{3}.10^{-3}\left(V\right)\)
\(Q=\frac{E_c^2}{R}t=\frac{\left(2\sqrt{3}.10^{-3}\right)^2}{10}.0,01=12.10^{-9}\left(J\right)\)
c/ \(I=\frac{E_c}{R+R'}=\frac{2\sqrt{3}.10^{-3}}{10+2}=\frac{\sqrt{3}.10^{-3}}{6}\left(A\right)\)
Check lại phần tính toán hộ mình nhé, nhiều số quá hơi nhức mắt :(
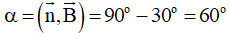
Đáp án C
Φ t r u o c = B S cos 0 ° = 0 , 01.0 , 05.0 , 05. cos 0 ° = 2 , 5.10 − 5 W b . Φ s a u = B S cos 90 ° = 0 , 01.0 , 05.0 , 05. cos 90 ° = 0 W b . Δ Φ = Φ s a u − Φ t r u o c = − 2 , 5.10 − 5 W b .