Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi 1g/ cm3 = 1000 kg / m3
Thả khối gỗ vào trong nước thì nổi \(\dfrac{1}{3}\) vậy thể tích phần gỗ chìm là \(\dfrac{2}{3}\)
Thả khối gỗ vào trong dầu thì nổi \(\dfrac{1}{4}\) vậy thể tích phần gỗ chìm là \(\dfrac{3}{4}\)
\(\Leftrightarrow F_{A_n}=d_n.\dfrac{2}{3}=1000.10.\dfrac{2}{3}\) (1)
\(\Leftrightarrow F_{A_d}=d_d.\dfrac{3}{4}\) (2)
Từ 1 - 2 => \(\dfrac{3}{4}D_d=\dfrac{2}{3}.1000\)
=> \(D_d=\dfrac{666}{0,75}=888\left(\dfrac{kg}{m^3}\right)\)
Cái này có vài chỗ làm tròn

-Nếu thả trong nước, phần chìm là:
\(V_{chìm1}=V-\frac{3}{5}V=\frac{2}{5}V\)
-Nếu thả trong dầu, phần chìm là:
\(V_{chìm2}=V-\frac{1}{2}V=\frac{1}{2}V\)
P=Fa nc
P=Fa dầu
=> Fa nc=Fa dau
<=> (2/5V).D nc=(1/2V).D dầu
=> D dầu= 800kg/m3

Em có thể chụp lại đề chị giải cho, đề này em đăng lỗi rồi em nha

Giải:
Đổi: Dnước=1g/cm3=1000kg/m3Dnước=1g/cm3=1000kg/m3
Gọi thể tích của khối gỗ là: V(m3)V(m3)
Thì thể tích phần gỗ chìm trong nước là:
V1=V−14.V=3V4(m3)V1=V−14.V=3V4(m3)
Và thể tích phần gỗ chìm trong dầu là:
V2=V−16.V=5V6(m3)V2=V−16.V=5V6(m3)
Do đó lực đẩy Ác si mét do nước tác dụng lên khối gỗ là:
FA1=dnước.V1=10.Dnước.3V4=30000V4FA1=dnước.V1=10.Dnước.3V4=30000V4
Và lực đẩy Ác si mét do dầu tác dụng lên khối gỗ là:
FA2=ddầu.V2=ddầu.5V6FA2=ddầu.V2=ddầu.5V6
Vì trong cả hai trường hợp thì khối gỗ đều nổi lên, nên khi đó thì trọng lượng của khối gỗ sẽ đúng bằng lực đẩy Ac-si-met tác dụng lên khối gỗ hay:
FA1=FA2=PFA1=FA2=P
⇔⇔ 30000V4=ddầu.5V630000V4=ddầu.5V6
⇔⇔ 90000V12=10ddầu.V1290000V12=10ddầu.V12
⇒90000V=10ddầu.V⇔ddầu=9000⇒90000V=10ddầu.V⇔ddầu=9000
Khối lượng riêng của dầu là:
Ddầu=ddầu10=900010=900(kg/m3

Gọi khối lượng gỗ: m (g)
thể tích gỗ: V (\(cm^{^{ }3}\))
Ta có:
+) Lực đẩy Acsimet khi thả vào nước: F1= D1. (V- \(\dfrac{3}{5}\).V)
+) Lực đẩy Acsimet khi thả vào dầu: F2= D2. (V- \(\dfrac{1}{2}\).V)
Theo nguyên lí cân bằng lực thì: m=F1 và m=F2
=> D1. (\(\dfrac{2}{5}\).V) = D2. (\(\dfrac{1}{2}\).V)
=> D2 = (\(\dfrac{2}{5}\).D1) / \(\dfrac{1}{2}\)
=> D2= \(\dfrac{4}{5}\).D1 = 0,8 (g)
Vậy khối lượng riêng của dầu là 0,8 g.
![]()

4. Trọng lượng giêng của nước là:
\(d=D.10=1000.10=10000\)(N/m3)
Theo công thức tính lực đẩy ác si mét ta có: \(F_A=d.V\)
nên thể tích của vật đó là: \(V=\dfrac{F_A}{d}=\dfrac{80000}{10000}=8\)(m3)
2. Gọi thế tích gỗ là V
Trọng lượng riêng của nước là D
Trọng lượng riêng của dầu là D'
Trọng lượng khối gỗ là P
Khi thả gỗ vào nước lực ác si mét tác dụng lên vật là: \(F_A=\dfrac{2.10D.V}{5}\)
Vì vật nổi lên ta có: \(F_A=P\Rightarrow\dfrac{2.10.D.V}{5}\) (1)
Khi thả khúc gỗ vào dầu lực ác - si - mét tác dụng lên vật là:
\(F_A'=\dfrac{1.10.D'.V}{2}\)
Vì vật nổi nên: \(F_A'=P=\dfrac{1.10.D'.V}{2}=P\) (2)
Từ (1) và (2) => \(F_A=F_A'\) hay \(\dfrac{2.10.D.V}{5}\) = \(\dfrac{1.10.D'.V}{2}\)
\(\Leftrightarrow8.10.D.V=9.10.D'.V\)
\(\Leftrightarrow D'=\dfrac{8.10.D.V}{9.10.V}=\dfrac{8}{9}.D\) (*)
Thay D = 1 kg/m3 vào (*) ta có:
\(D'=\dfrac{8}{9}.1=\dfrac{8}{9}\) kg/m3
Vậy khối lượng riêng của dầu là \(\dfrac{8}{9}\approx0,89\)kg/m3

Khi khối gỗ nổi trong chất lỏng thì trọng lượng của khối gỗ cân bằng với lực đẩy Ácsimét. Mặt khác, vì trọng lượng của khối gỗ không thay đổi nên lực đẩy Ácsimét do chất lỏng tác dụng lên khối gỗ trong hai trường hợp vẫn không đổi
Theo công thức \(F_A=d.V\Rightarrow d=\dfrac{F_A}{V}\) Thì trọng lượng riêng của chất lỏng tỉ lệ nghịch với thể tích của phần chất lỏng bị vật chiếm chỗ
Gọi trọng riêng của nước là \(d_1\), của dầu là \(d_2\). Gọi phần thể tích của khối gỗ nổi trong nước \(V_{n1}\) , nổi tỏng dầu là \(V_{n2}\) , phần Thể tích của khối gỗ chìm trong nước là \(V_{c1}\) , chìm trong dầu là \(V_{c2}\)
Vậy nên
\(\dfrac{d_1}{d_2}=\dfrac{V_{c1}}{V_{c2}}\Rightarrow\dfrac{d_1}{d_2}=\dfrac{V_{c2}}{V-V_{n1}}\Rightarrow\dfrac{d_1}{d_2}=\dfrac{V_{c2}}{V-\dfrac{V}{3}}\\ \Rightarrow\dfrac{d_1}{d_2}=\dfrac{3V_{c2}}{2V}\Rightarrow V_{c2}=\dfrac{5V}{6}\)
Phần thể tích nổi trên dầu là
\(V_{n2}=V-V_{c2}=V-\dfrac{5V}{6}=\dfrac{1}{6}V\)

Gọi m, V, D lần lượt là khối lượng, thể tích, khối lượng riêng của vật.
Khi thả vật rắn vào bình đầy nước hoặc bình đầy dầu thì có một lượng nước hoặc một lượng dầu ( có cùng thể tích với vật ) tràn ra khỏi bình.
Độ tăng khối lượng của cả bình trong mỗi trường hợp:
m1 = m – D1V (1)
m2 = m– D2V (2)
Lấy (2) – (1) ta có:
m2 – m1 = V(D1 – D2)
\(\Rightarrow V=\frac{m_2-m_1}{D_1-D_2}=300\) (cm3)
Thay giá trị của V = 300 cm3 vào (1), ta đc:
\(m=m_1+D_1V=321,75\left(g\right)\)
Từ công thức \(D=\frac{m}{V}\), ta có:
\(D=\frac{m}{V}=\frac{321,75}{300}\approx1,07\left(g\right)\)
Bạn xem lời giải của mình nhé:
Giải:
Gọi m, V, D lần lượt là khối lượng, thể tích, khối lượng riêng của vật.
Khi thả vật rắn vào bình đầy nước hoặc bình đầy dầu thì có một lượng nước hoặc một lượng dầu ( có cùng thể tích với vật ) tràn ra khỏi bình.
Độ tăng khối lượng của cả bình trong mỗi trường hợp:
m1 = m – D1.V (1)
m2 = m – D2.V (2)
Lấy (2) – (1) ta có: m2 – m1 = V.(D1 – D2)
\(\Rightarrow V=\frac{m_2-m_1}{D_1-D_2}=300\left(cm^3\right)\)
Thay giá trị của V vào (1) ta có : \(m=m_1+D_1.V=321,75\left(g\right)\)
Từ công thức \(D=\frac{m}{V}=\frac{321,75}{300}\approx1,07\)(g/cm3)
Vậy V = 300 cm3
m = 321,75g
\(D\approx\) 1,07g/cm3
Chúc bạn học tốt!![]()
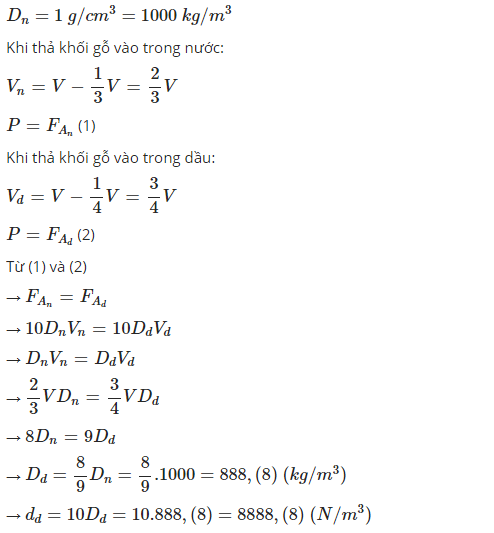
800
800