Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu: \(C_{15}^4\)
a.
Số cách lấy 4 viên bi trong đó có 3 viên màu đỏ: \(C_7^3C_8^1\)
Xác suất: \(P=\dfrac{C_7^3.C_8^1}{C_{15}^4}\)
b.
Lấy 4 viên không có viên đỏ nào (lấy từ 8 viên 2 màu còn lại): \(C_8^4\) cách
Lấy 4 viên có ít nhất 1 viên đỏ: \(C_{15}^4-C_8^4\)
Xác suất: \(P=\dfrac{C_{15}^4-C_8^4}{C_{15}^4}\)
c.
Các trường hợp thỏa mãn: (2 đỏ 1 xanh 1 vàng), (1 đỏ 2 xanh 1 vàng), (1 đỏ 1 vàng 2 xanh)
Số cách lấy: \(C_7^2C_5^1C_3^1+C_7^1C_5^2C_3^1+C_7^1C_5^1C_3^2\)
Xác suất: \(P=\dfrac{C_7^2C_5^1C_3^1+C_7^1C_5^2C_3^1+C_7^1C_5^1C_3^2}{C_{15}^4}\)

Gọi A là biến cố: “trong số 7 viên bi được lấy ra có ít nhất 1 viên bi màu đỏ.”
Trong hộp có tất cả: 5+ 15 + 35 = 55 viên bi
- Số phần tử của không gian mẫu: Ω = C 55 7 .
- A ¯ là biến cố: “trong số 7 viên bi được lấy ra không có viên bi màu đỏ nào.”
=> n A ¯ = C 20 7 .
Vì A và A ¯ là hai biến cố đối nên: n A = Ω − n A ¯ = C 55 7 − C 20 7 .
Xác suất để trong số 7 viên bi được lấy ra có ít nhất 1 viên bi màu đỏ là P A = C 55 7 − C 20 7 C 55 7 .
Chọn đáp án B.

Gọi A là biến cố lấy ra được 3 viên bi màu đỏ.
Số cách lấy 3 viên bi từ 20 viên bi là C 20 3 nên ta có Ω = C 20 3 = 1140 .
Số cách lấy 3 viên bi màu đỏ là C 8 3 = 56 nên Ω A = 56 .
Do đó: P ( A ) = 56 1140 = 14 285
Đáp án B

Ta có, số phần tử của không gian mẫu n ( Ω ) = C 10 2
Gọi các biến cố: D: “lấy được 2 viên đỏ” ; X: “lấy được 2 viên xanh” ;
V: “lấy được 2 viên vàng”
Ta có D, X, V là các biến cố đôi một xung khắc và C = D ∪ X ∪ V
P ( C ) = P ( D ) + P ( X ) + P ( V ) = C 4 2 C 10 2 + C 3 2 C 10 2 + C 2 2 C 10 2 = 2 9
Chọn đáp án B

Không gian mẫu: \(C_{14}^5\)
Các cách chọn thỏa mãn gồm có: (1 đỏ 1 vàng 3 xanh), (2 đỏ 1 vàng 2 xanh), (1 đỏ 2 vàng 2 xanh)
Số cách: \(C_5^1C_6^1C_3^3+C_5^2C_6^1C_3^2+C_5^1C_6^2C_3^2\)
Xác suất: \(P=\dfrac{C_5^1C_6^1C_3^3+C_5^2C_6^1C_3^2+C_5^1C_6^2C_3^2}{C_{14}^5}=...\)
Quảng cáo trắng trợn ghê tar :3 Cơ mà có mod Lâm là đủ rồi á THẦY :)

Ta có: ![]()
Gọi các biến cố: D: “lấy được 2 bi viên đỏ” ta có ![]()
X: “lấy được 2 bi viên xanh” ta có: ![]()
V: “lấy được 2 bi viên vàng” ta có: ![]()
T: “ lấy được 2 bi màu trắng” ta có : ![]()
Ta có D; X; V; T là các biến cố đôi một xung khắc và A= D ∪ X ∪ V ∪ T
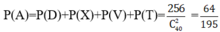
Chọn B.

Đáp án B
Hướng dẫn giải:
+ Số cách chọn 1 viên bi xanh: ![]()
+ Số cách chọn 2 viên bi đỏ: ![]()
+ Số cách chọn 5 viên bi trắng: ![]()
+ Số cách chọn 8 viên bi thỏa mãn yêu cầu bài toán: ![]()
 .
.