Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thể tích hình trụ : V 1 = πr 2 h = πr 2 .3r = 3 πr 3 (đvdt)
Thể tích hình cầu : V 2 = (4/3). πr 3 (đvdt)
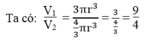
Vậy chọn đáp án B

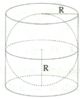
a) Hình cầu bán kính r, vậy thể tích của nó là 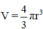
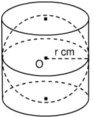
b) Hình trụ có bán kính đáy bằng r và chiều cao bằng 2r
Vậy thể tích của nó là: V 1 = π r 2 ⋅ 2 r = 2 π r 3
c) Thể tích hình trụ trừ đi thể tích hình cầu là:
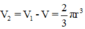
d) Thể tích hình nón có bán kính đáy r, chiều cao 2r
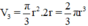
e) Từ các kết quả trên suy ra: Thể tích hình nón "nội tiếp" trong một hình trụ thì bằng thể tích hình trụ trừ đi thể tích hình cầu nội tiếp trong hình trụ ấy.
Hoặc: Thể tích hình trụ bằng tổng thể tích hình nón và hình cầu nội tiếp hình trụ.
Ta có \(V_{cầu}=\frac{4}{3}.\pi.R^3=\frac{4}{3}.\pi.\left(\frac{6}{2}\right)^3\)
\(=\frac{4}{3}.\pi.3^3\)
\(=4.\pi.9=36\pi\left(dm^3\right)\approx113dm^3\)
Ta thấy \(113dm^3>35dm^3\) nên thể tích hình cầu lớn hơn thể tích hình trụ