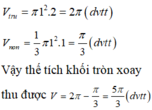

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Khi quay quanh CD sẽ tạo ra hình khối gồm 2 khối:
- Khối trụ chiều cao \(AB=a\) bán kính đáy \(r=AD=a\Rightarrow V_1=\pi.AB^2.AD^2=\pi a^3\)
- Khối nón chiều cao \(CH=\dfrac{1}{2}CD=a\) bán kính đáy \(BH=AD=a\Rightarrow V_2=\dfrac{1}{3}\pi.a^2.a=\dfrac{\pi a^3}{3}\)
\(\Rightarrow V=V_1+V_2=\pi a^3+\dfrac{\pi a^3}{3}=\dfrac{4\pi a^3}{3}\)

Đáp án A
Lấy I là trung điểm CD. Thể tích vật tròn xoay là
π . π . π 2 + 1 3 π . π . π 2 = 4 3 π 4

Đáp án A
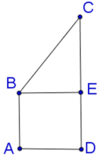
Khi quay hình thang quanh AB , ta được khối tròn quay có thể tích băng thể tích hình trụ bán kính đáy AD , chiều cao CD trừ đi thể tích hình nón có bán kính đáy AD , chiều cao CE.
Dễ dàng tính được CE=1.
Ta có: