Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chiều rộng là x
Chiều dài là x+6
Theo đề, ta có: 4(x+6)-x=51
=>4x+24-x=51
=>3x+24=51
=>x=9
Chiều dài là 9+6=15(m)
Chu vi là (15+9)x2=48(m)
Diện tích là 15x9=135(m2)

nếu tăng chiều dài thêm 15cm và giữ nguyên chiều rộng thì diện tích tăng thêm 150cm² thì chiều rộng của hình chữ nhật đó là:
150:15=10(cm)
chiều dài hình chữ nhật đó là:
10x3=30(cm)
diện tích ban đầu của hình chữ nhật đó là:
10x30=300(cm²)

Đổi gấp rưỡi = 1,5= 15/10= 3/2
Nửa chu vi hình chữ nhật là:
400:2=200 (m)
Chiều dài cái ao hình chữ nhật là:
200:(3+2)x3=120
Diện tích cái ao hình chữ nhật là:
120x(200-120)=9600 (m2)
Diện tích của cái ao là:
9600:100x3=288 (m2)
Vậy diện tích còn lại của mảnh vườn bằng:
9600-288=9312 (m2)
Từ một điểm S ở ngoài đt (o) kẻ tiếp tuyến SA và một các tuyến SBC ( góc BAC <90) Phân giác góc BAC cắt BC tại D và cắt đt tại điểm thứ hai là E Cac tiếp tuyến của đt (o) tại C và E cắt nhau tại N. P là giao điểm AE và CN
CM a ) SA =SD B) EN//BC C) \(\frac{1}{cn}=\frac{1}{cp}+\frac{1}{cd}\) ANH CHỊ GIÚP E VỚI Ạ CÂU C Í Ở MATHONLINE KHÔNG AI GIÚP EM MỚI SANG ĐÂY

Đáp án: D
Gọi chiều dài, chiều rộng của mảnh vườn lần lượt là ![]() (m)
(m) ![]()
Theo đề bài ta có:  là nghiệm của phương trình
là nghiệm của phương trình ![]()

- Diện tích hình chữ nhật lớn nhất trong $(P)$ khi chiều dài bằng chiều rộng.
- Vậy diện tích hình chữ nhật lớn nhất là: $2.2=4(m^2)$

Đáp án: A
Gọi chiều dài, chiều rộng của mảnh vườn lần lượt là ![]() (m)
(m) ![]()
Theo đề bài ta có:
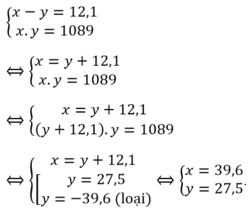

Đáp án: B
Giả sử x = 25 + a; y = 42 + b; -0,01 ≤ a, b ≤ 0,01
Diện tích hình chữ nhật là S = (25 + a)(42 + b) = 1050 + 42a + 25b + ab
Do-0,01 ≤ a, b ≤ 0,01
⇒ |42a + 25b + ab| ≤ 42.0,01 + 25.0,01 + 0,01.0,01
⇒ |42a + 25b + ab| ≤ 0,6701
⇒ |S - 1050| ≤ 0,6701
⇒ S = 1050 + 0,6701m2

Theo giải thiết ta có tam thức sau: \(f\left( x \right) = 20.15 - \left( {20 + x} \right)\left( {15 - x} \right) = {x^2} + 5x\)
Tam thức có \(\Delta = 25 > 0\), có hai nghiệm phân biệt \({x_1} = 0;{x_2} = -5\)
Vậy khoảng diện tích tăng lên là \(x>0\) và \(x<-5\), khoảng diện giảm đi là \(x \in(-5;0)\) và diện tích không đổi khi \(x = 0\) và \(x = -5\)
50*2*3=