Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

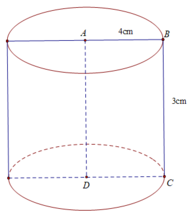
a) Diện tích xung quanh của hình trụ bằng:
S x q = 2πRh = 2π.4.3 = 24π ( c m 2 )

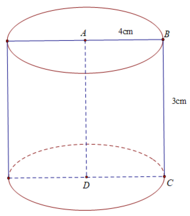
b) Thể tích hình trụ bằng :
V = π R 2 h = π 4 2 .3 = 48π( c m 3 )

1:
V=pi*r^2*h
=>r^2*15*pi=375pi
=>r^2=25
=>r=5
Sxq=2*pi*r*h=2*5*15*pi=150pi

Hướng dẫn làm bài:
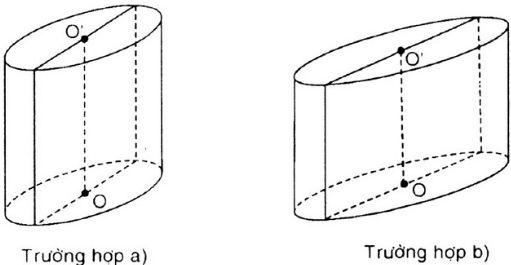
Bài toán có 2 trường hợp
a) Đường cao của hình trụ bằng 3cm. Khi đó chiều rộng của hình chữ nhật là đường kính của hình trụ, suy ra R = 1cm
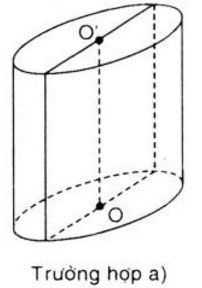
Vậy Sxq = 2πRh = 2π .1 .3 = 6π (cm2)
V = πR2h = π. 12 . 3 = 3π (cm3)
b) Đường cao hình trụ bằng 2cm
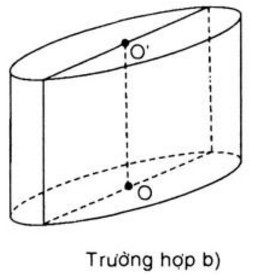
khi đó chiều dài của hình chữ nhật là đường kính của hình trụ, suy ra R = 1,5
Vậy Sxq = 2πRh = 2π . 1,5 . 2 = 6π (cm2)
V = πR2h = π . 1,52 . 2 = 4,5 π (cm2)
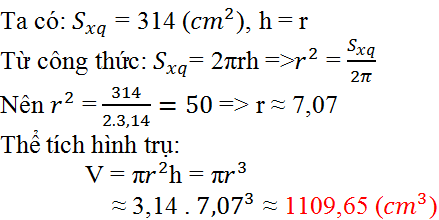

Lời giải:
Giả thiết hình chữ nhật nằm ngang.
Quay một vòng quanh chiều dài cố định là thu được một hình trụ có bán kinh đáy $r$ bằng chiều rộng, chiều cao $h$ bằng chiều dài
Vì chiều dài gấp đôi chiều rộng nên \(h=2r\)
Diện tích xung quanh của hình trụ:
\(S_{xq}=2\pi rh=100\pi\)
\(\Leftrightarrow 2\pi.r.2r=100\pi\)
\(\Leftrightarrow r^2=25\Rightarrow r=5\) (cm)
Do đó \(h=2r=10(cm)\)
Giả thiết hình chữ nhật nằm ngang.
Quay một vòng quanh chiều dài cố định là thu được một hình trụ có bán kinh đáy rr bằng chiều rộng, chiều cao hh bằng chiều dài
Vì chiều dài gấp đôi chiều rộng nên h=2rh=2r
Diện tích xung quanh của hình trụ:
Sxq=2πrh=100πSxq=2πrh=100π
⇔2π.r.2r=100π⇔2π.r.2r=100π
⇔r2=25⇒r=5⇔r2=25⇒r=5 (cm)
Do đó h=2r=10(cm)