Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án B.
Phương pháp
+) Xác định bán kính đáy và chiều cao hình trụ.
+) Tính thể tích khối trụ
+) Tính tổng thể tích 7 viên bi, từ đó suy ra thể tích lượng nước cần dùng.
Cách giải
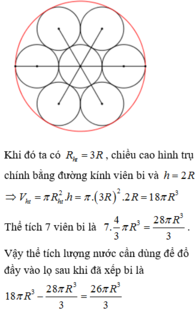
Ta mô phỏng hình vẽ đáy của hình trụ như sau:
Đáp án C.
Dễ thấy bán kính đáy của cái lọ bằng 3r.
Do đó diện tích đáy S của cái lọ bằng S = π 3 r 2 = 9 π r 2 .
Đáp án D
Bán kính đáy của cái lọ là R = 3 r ⇒ S = π R 2 = π 3 r 2 = 9 π r 2
Đáp án B
Phương pháp:
- Gắn hệ trục tọa độ Oxy, xác định phương trình hàm số bậc ba.
- Ứng dụng tích phân vào tính thể tích.
Cách giải:
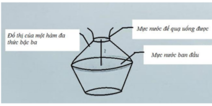
Gắn hệ trục tọa độ Oxy như hình vẽ.
Gọi phương trình của đường sinh là: 
Theo đề bài, ta có: (C) có điểm cực đại (0;3), điểm cực tiểu là (2;1)
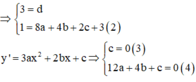
Từ (1),(2),(3) và (4)
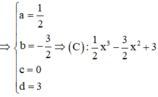
Thể tích đã cho vào:
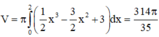
Thể tích 1 viên bi là
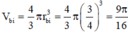
Cần số viên bi: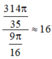 
(viên)
Đáp án D.
Khối nón cụt có thể tích là V = πh 3 R 2 + R . r + r 2 mà h = 3 V = π ⇒ R 2 + R . r + r 2 = 1 (*).
Ta có P = R + 2 r ⇔ R = P - 2 r thay vào (*), ta được P - 2 r 2 + P - 2 r r + r 2 = 1
⇔ P 2 - 4 P r + 4 r 2 + P r - 2 r 2 + r 2 - 1 = 0 ⇔ 3 r 2 - 3 P r + P 2 - 1 = 0 (I).
Vậy phương trình (I) có nghiệm khi và chỉ khi ∆ I = - 3 P 2 - 4 . 3 . P 2 - 1 ≥ 0 ⇔ P ≤ 2 .
Vậy giá trị lớn nhất của P là 2.
Đáp án B
Thể tích của mỗi thỏi son hình trụ là:
V = π r 2 h = 20 , 25 π ⇔ r 2 h = 20 , 25 ⇔ h = 20 , 25 r 2
Ta có:
T = 60000 r 2 + 20000 r h = 60000 r 2 + 20000 r . 20 , 25 r 2 = 60000 r 2 + 405000 r
60000 r 2 + 202500 r + 202500 r ≥ 3 60000 r 2 . 202500 r . 202500 r 3 = 405000
Dấu “=” xảy ra khi:
60000 r 2 = 202500 r ⇔ r = 3 2 ⇒ h = 9 ⇒ r + h = 10 , 5 c m
Theo công thức ta có:
Sxq = 2πrh = 2√3 πr2
Stp = 2πrh + 2πr2 = 2√3 πr2 + 2 πr2 = 2(√3 + 1)πr2 ( đơn vị thể tích)
b) Vtrụ = πR2h = √3 π r3
c) Giả sử trục của hình trụ là O1O2 và A nằm trên đường tròn tâm O1, B nằm trên đường tròn tâm O2; I là trung điểm của O1O2, J là trung điểm cảu AB. Khi đó IJ là đường vuông góc chung của O1O2 và AB. Hạ BB1 vuông góc với đáy, J1 là hình chiếu vuông góc của J xuống đáy.
Ta có là trung điểm của
,
= IJ.
Theo giả thiết = 300.
do vậy: AB1 = BB1.tan 300 = = r.
Xét tam giác vuông
AB1 = BB1.tan 300 = O1J1A vuông tại J1, ta có: =
-
.
Vậy khoảng cách giữa AB và O1O2 :
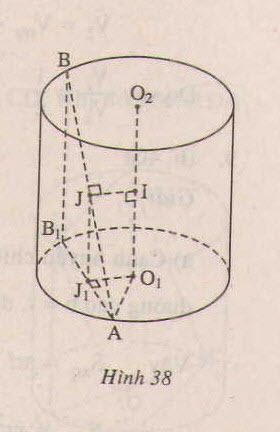
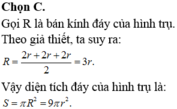
Đáp án A
Ta có: V T = πR 2 h = 16 π ⇒ R 2 h = 16
Diện tích nguyên liệu cần dung là: S = 2 πR 2 + 2 πRh = 2 π R 2 + 16 R . Lại có R 2 + 16 R = R 2 + 8 R + 8 R ≥ 3 8 2 3 .
Dấu bằng xảy ra ⇔ R = 2 .